把研究对象、状态、过程等建立物理模型
物理学所分析和研究的实际问题往往非常复杂,有众多的因素,如果我们把所有的因素都毫不遗漏地考虑进去,那么势必会增加研究问题的难度,甚至无法研究。因此,为了更好地揭示事物的本质,人们往往根据观察和实验所获得的各种感性材料,将复杂具体的物理事件去粗存精(舍去那些表面的、次要的条件,抓住主要因素),得出一种能反映原物本质特性的理想物质(过程)或假想结构,这种理想物质(过程)或假想结构就称之为物理模型。物理模型是人们通过科学思维对物质世界中原物的抽象描述;是按照物理学研究的特定目的,用物质形式或思维形式对原型客体本质关系的再现。人们通过对物理模型的认识与研究,去获取关于原型客体的知识及其在自然界中的运动变化规律。在解答物理问题时,关键点在于:一是要明确研究对象是什么以及研究对象所处的状态,并把研究对象视为适当的模型;二是要研究状态如何变化,即所谓过程,并把它视为适当的模型,然后找出这些模型所遵循的规律。
由于具体物理问题的解决,需要把具体的物理现象和过程还原成一定的“物理模型”,才能用相应的规律或理论加以解决,因此“物理模型”教学是提高学生分析问题能力的重要途径,也是培养学生科学研究物理问题的有效途径。同时,通过“物理模型”教学,还有利于促使教学的软化,促进学生综合素质的提高。
在科学研究和物理教学中物理模型的建立具有十分重要的作用。利用理想模型,可以使复杂问题的处理大为简化而又不会发生大的偏差;同时,可使事物的运动规律具有较为简单的形式,让人们更好地认识和掌握。物理模型教学对于培养学生的抽象思维能力、分析解决问题的能力和应试能力等方面是极为有利的,物理模型教学是教师传授物理知识的一种基本方法,也是学生获取物理知识的重要途径,物理模型的建立在物理教学中具有重要作用。
例1一架老式飞机在高出地面H的高度,以速度v水平飞行,为了使飞机上投下的炸弹落在指定的目标上,应该在距离轰炸目标多远的地方投弹?
解决该问题时,必须舍弃次要因素——空气阻力的影响,建立相应的物理模型。由于炸弹从水平飞行的飞机上落下,再离开飞机时具有与飞机相同的水平速度,因而可把炸弹近似作为平抛物体运动。炸弹同时参与竖直方向的自由落体运动和水平方向的匀速直线运动。轰炸目标在地面上,炸弹落到地面所用的时间t是由竖直方向的运动决定的,在时间t内,如果炸弹在水平方向通过的距离等于飞机投弹时离目标的水平距离,即可命中目标。
例2一跳水运动员从离水面10m高的平台跃起,举起双臂直体离开平台,此时重心位于从手到脚全长的中点,跃起后重心升高0.45m达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向运动忽略不计)。从离开平台到手触水面,问他可用于完成空中各种动作的时间是多少。
表面上看,这个问题比较复杂,但是只要抓住主要因素(运动员竖直跃起到最高点,然后再跳入水中这一过程),首先把结构复杂的人体抽象成一个质点,建立质点模型;然后忽略运动员在水平方向的运动,这样跳水运动员的跳水过程就可以看成竖直上抛过程,建立竖直上抛运动模型。实际上本题已经建立了两个模型:一是质点模型;二是竖直上抛运动模型。根据题意建立起物理模型,利用相应的物理模型的规律便可轻松求解。
例3某学校科技小组的同学们设计了一个自动冲刷厕所的水箱模型,这种水箱模型能把自来水管供给的较小流量的水储存到一定量后,自动开启放水阀门,冲刷便池中的污物。如图10-1是这种水箱模型的主要部件的截面示意图,图10-1中水箱A是一个底面积为200cm2的圆柱桶,桶的深度为60cm,上面敞口。浮筒B是一个质量为m=0.2kg的空心密封圆柱体,其底面积S1为80cm2,高为30cm;放水阀门C是一个质量可忽略的圆柱体,其底面积S2为40cm2,厚度d为1cm;放水阀门C能将排水管口恰好盖严,阀门上固定一根轻杆与浮筒相连,杆的长度为L,当水箱中的水深达到H时,浮筒B刚好能将放水阀门C打开。
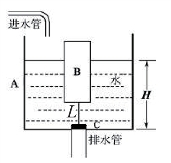
图10-1
(1)请求出水箱中的水深H与轻杆L的函数关系。
(2)求当L为多长时,进水管不管进水多长时间也无法把阀门C打开。
【考点】浮力大小的计算;力的合成与应用。
【分析】(1)当浮筒B所受的浮力大于B的重力与杆的拉力之和时才能将阀门打开,设浮筒B浸入水中深度至少为h时阀门C刚好被打开,根据受力分析与浮力的计算公式求出h,则H=h+d+L;
(2)当浮筒B全部浸没时浮力仍小于或等于B的重力与杆的拉力之和时,不管进水多长时间都无法把阀门C打开;由(1)中H与L的关系以及H≤30cm+L+d,求出L的长度。
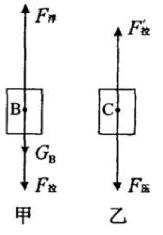
图10-2
【解答】由题知:H=60cm;mB=0.2kg;S1=80cm2;hB=30cm;S2=40cm2;d=1cm;
(1)设浮筒B浸入水中的深度至少为h时阀门C刚好被打开;方法一:以B为研究对象,受力分析如图甲所示:F浮=GB+F拉,以C为研究对象,受力分析如图乙所示:F拉′=F压,
因为F拉=F拉′,所以F浮=GB+F压,
即:ρ水gS1h=mBg+ρ水gS2(h+L)。
代入数据解得:h=5+L。
则水深为:H=h+L+d。
即:H=2L+6cm。
方法二:以B和C整体作为研究对象ρg(H-L-d)S1-ρg(H-d)S2=mg,
代入数据得:H=2L+6cm。
(2)根据题意可知:H≤30cm+L+d,H≤60cm,H=2L+6cm。
由以上三式得L≤25cm。
答:(1)水箱中的水深H与轻杆L的函数关系是:H=2L+6cm。
(2)当L≤25cm时,进水管不管进水多长时间也无法把阀门C打开。
【点评】考查(1)对物体进行受力情况分析;(2)液体内部压强公式;(3)压强的定义式;(4)阿基米德原理;(5)运用物理知识解决生产、生活中实际问题的能力,综合性强,难度大。
