巧用数学知识解决物理问题
最近几年全国各省（市、省治区）物理中考命题中，越来越注重利用数学方法解决物理问题的考查，这就提醒我们一线的教师对于隐藏在物理问题中的数学方法，要在平时教学过程中传授给学生，在教学生掌握基础物理知识的同时，重视培养用数学知识解决物理问题的能力。
在数学中，若一个量的变化引起另一个量的变化，并且遵从一定的变化规律，这两个量之间的相互变化关系我们称为函数关系。我们所学过的函数有：一次函数、二次函数、三角函数等。数学中，将形如“y=kx+b（k≠0，b为常数）”的函数称为（y关于x的）一次函数。物理很多规律都呈现一次函数的关系，而且一次函数学生容易分析与计算，利用待定函数法和一次函数解答很多物理问题十分快捷。因此，最近几年，全国很多省（市、省治区）中考命题中，开始出现运用一次函数法解题的题型。他山之石，可以攻玉。下面以北京市和昆明市最近几年的中考试题为例，对应该如何更快更巧妙地利用一次函数解决物理问题进行分析与探讨。
例1小莉把一圆柱形物体挂在弹簧测力计的挂钩上，将圆柱形物体逐渐浸入某种液体中，观察并记录物体排开液体的体积V和弹簧测力计的示数F，得到如下表所示的实验数据。请根据表中数据归纳出F与V的关系，
F= __________________。
分析：分析表中的数据可知，物体排开液体的体积V每增大1×10-4 m3，弹簧测力计的示数F减小0.8 N， F与V的变化成线性关系。本题应从计算浮力的两种方法入手，根据弹簧测力计的示数F=G-F浮、阿基米德原理F浮=ρ液gV排，将表格中数据代入关系式求解。
解答：由题意知：F=G-F浮，F浮=ρ液gV，
故F=G-ρ液gV。
将第一、二组数据代入可得：
4.2N=G-ρ液g×1×10-4m3， （1）
3.4N=G-ρ液g×2×10-4m3。 （2）
由⑴式－⑵式，可得：ρ液=0.8×103kg/m3，G=5N；
则F=G-F浮=5N-800kg/m3×10N/kg×V=5N-8000N/m3·V。
故答案为：F=5N-8000N/m3·V。
点 评
此题考查了对实验数据的分析，掌握浮力、拉力、重力的关系，根据数据得出重力和液体密度的大小是解决此题的关键。
例2如下表是小丽在实验中记录的实验数据，请根据表格中的数据归纳出电功率P和电阻R的关系：P＝______________________。
分析：分析表中的数据可知，电阻R每增大5Ω时，电路中的总功率减小0.2W，电阻的电功率随电阻的变化成线性关系，设出它们之间的关系，从表格中找出任意两组数据代入表达式即可得出答案。
解答：分析表中的数据可知，电阻的电功率随电阻的变化成线性关系，设P=kR+b，
当R=5Ω时，P=2.6W；当R=10Ω时，P=2.4W，
则2.6W=k×5Ω+b， （3）
2.4W=k×10Ω+b。 （4）
解得：k=-0.04，b=2.8W。所以电功率P和电阻R的关系式：P=2.8W-0.04（W/Ω）·R。故答案为：2.8W-0.04（W/Ω）·R。
点 评
本题是探究电功本题是探究电功率与电阻之间的关系，要求考查了对实验数据的分析，要学会从数据中总结规律性的结论。
例3摄氏温度的规定：在一个标准大气压下，纯净的冰水混合物的温度定为0℃，水沸腾时的温度定为100℃。将0～100℃之间划分为100等分，每一等分就是1℃。华氏温度的规定：在一个标准大气压下，纯净的冰水混合物的温度定为32
，读作华氏度），水沸腾时的温度定为212
。将32～212
之间划分为180等份，每一等份就是l
。则华氏度F与摄氏度t之间的关系是F= ______________
，人的正常体温大约为______℃。
分析：由题意可求出1摄氏度等于多少华氏度；最后即可求出摄氏度与华氏度之间的关系；人的正常体温大约为37℃。
解答：（1）∵华氏温标规定：1标准大气压下沸水的温度为212华氏度，冰水混合物的温度是32华氏度，中间分为180等份，每一等份代表1华氏度，
∴摄氏温差100度等同华氏温差180度，
即1摄氏度=180/100华氏度=1.8华氏度。
又知：华氏温度起点为32华氏度等于摄氏温度的0度，
所以，华氏温度与摄氏温度之间的关系为：T=1.8t+32。
（2）人的正常体温大约为37℃。
故答案为：T=1.8t+32；37。
点 评
热力学温标和摄氏温标的关系T=t+273；华氏温标跟它们的最大区别就是分度值不同。本题涉及考点是摄氏温度及其计算，温度计、熔化和凝固的知识。
例4某实验小组用水、刻度尺、弹簧测力计和圆柱体探究浮力与深度的关系，他们分别记录了不同情况下弹簧测力计的大小（如表所示），表中h表示圆柱体下表面浸入水中的深度。
（1）当h=0.05m时，圆柱体受的浮力是__________N。
（2）圆柱体完全没入水中前，弹簧测力计的拉力F与圆柱体下表面浸入水中深度h的关系F=__________________。
分析：（1）由表中数据可知，当h=0时，F为10N，即圆柱体重力为10N；当h=0.05m时，F为7.5N，则F浮=G-F。
（2）分析表中数据可知，圆柱体全部入水之前下表面浸入水中的深度每增加1cm，弹簧测力计示数F减小0.5N，F与h的变化成线性关系，进一步归纳得出表达式。
解答：（1）由表中数据可知，圆柱体重力G=10N；当h=0.05m时，F=7.5N。
此时F浮=G-F=10N-7.5N=2.5N。
（2）分析表中数据可知，h=0.08m之后F不变，浮力不变，圆柱体完全没入水中。圆柱体全部入水之前下表面浸入水中的深度每增加1cm，
弹簧测力计示数减小ΔF=10N-9.5N=9.5N-9N=9N-8.5N=8.5N-8N=8N-7.5N=7.5N-7N=7N-6.5N=0.5N，
即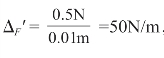
，
故表达式可写为F=10N-50N/m·h。
故答案为：2.5；F=10N-50N/m·h（h≤0.08m）。
点 评
本题中第二问是难点，利用F浮=G-F求浮力，先要找出浮力大小与圆柱体浸入水中深度的变化规律，再确定浸没前弹簧测力计的拉力与浸入水中深度的关系。
使用一次函数解题时，必须要看一个量的变化引起另一个量的变化（自变量与因变量）是不是线性关系，这是前提。如果不是线性关系，则此法不能使用。通过以上4个例题的分析我们不难发现，这些题目都运用到了一次函数的函数特性去解决物理问题，但是问题的突破其实还是要求学生从最基本的物理关系入手，善于摆脱传统的思维模式，从基本关系式中剥离出相关物理量的函数关系，从而最终在函数的特性基础上，实现对问题的解决与突破。