4.2.3 计量结果与讨论
1)实证结果分析
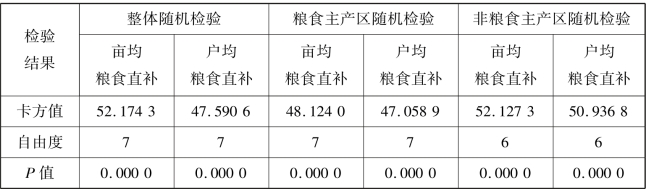
关于面板模型,首先采用Hausman检验确定应选择随机效应模型还是固定效应模型。为全面分析粮食直补对粮食作物播种面积的影响,本章将粮食直补分别用亩均粮食直补和户均粮食直补来进行Hausman检验,结果如表4.3所示。无论是每亩粮食直补还是每户粮食直补,Hausman检验统计量在显著水平为1%时都拒绝原假设,即个体效应和解释变量无关,应抛弃随机效应模型,即两种粮食直补政策的效果分析均须采用固定效应模型。此外,无论是粮食主产区还是非粮食主产区的Hausman检验,都在1%的显著水平下拒绝原假设,因此,在进行粮食主产区和非粮食主产区粮食直接补贴对粮食作物播种面积的影响分析时也采用固定效应模型。
表4.3 Hausman检验结果
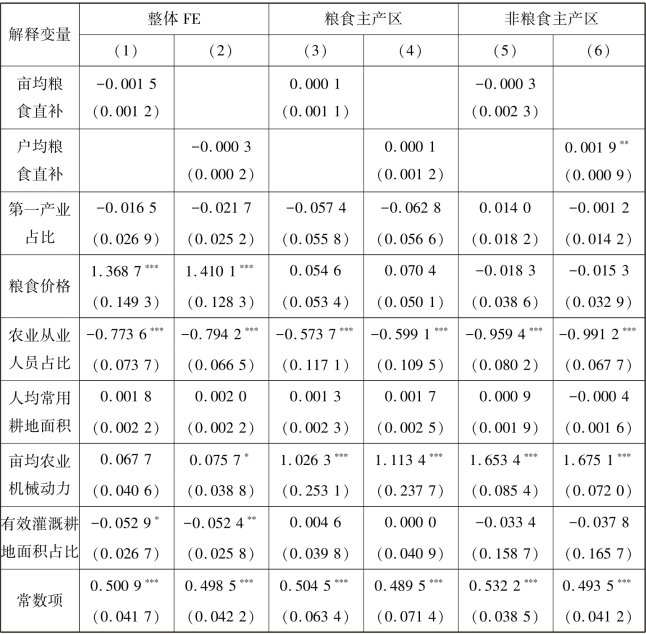
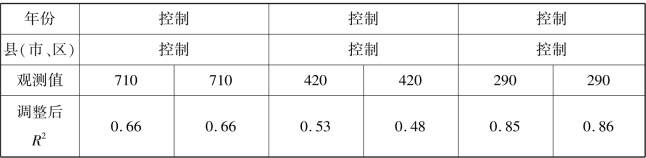
粮食直接补贴对粮食作物播种面积并不存在显著影响。由表4.4可知,整体样本的固定效应模型的估计结果与前文讨论的描述性分析结果是一致的。无论是亩均粮食直补还是户均粮食直补,都没有通过显著性检验,且粮食直补的估计系数为负,表明随着粮食补贴资金的增加,播种面积将减少。但值得注意的是,粮食直接补贴对粮食作物播种面积的负影响非常小,估计系数值几乎接近0,尤其是每户粮食直补(在整体样本情况下,每亩粮食直补对粮食作物播种面积的影响系数值大于每户粮食直补的影响系数值)。这说明粮食直接补贴对粮食作物播种面积并不存在显著影响,即粮食直接补贴不影响农户扩大播种规模的意愿,这与黄季焜和王晓兵等的研究(2011)相一致,并从实证角度在一定程度上印证了假说4.1的正确性。
表4.4 粮食直接补贴对粮食作物播种面积影响的固定效应模型估计结果
续表
注:*,**和***分别表示在10%、5%和1%的水平上显著;括号内数字为标准差。
粮食直补无法促进播种面积比例增加的原因可能有三:
首先,粮食直补的发放往往发生在粮食播种之后,属于事后的激励。关于粮食直补,农户往往会选择进行消费而非用于生产。因此,粮食直补对农户当年的播种意愿没有影响,而且对第二年扩大粮食种植规模具有较小的影响。
其次,粮食直补的资金较少,农户的机会成本较高。即使粮食直补对粮食作物播种面积具有一定的激励作用,能够促使粮食作物播种面积扩大,但粮食的种植、管理、收割等需要消耗更多的劳动力和生产资料,而同期粮食作物的价格却比较平稳,相比农户的工资性收入来说,机会成本高,因此农户往往对扩大粮食规模的热情度不高。
最后,粮食生产规模和面积与粮食直补脱钩。从政府部门角度分析,粮食直补的发放具有一定的衡量标准,然而实际操作中,粮食直补衡量标准的成本较高。一方面,上级政府部门需要依靠基层组织,而基层组织往往选择多报,导致大量的粮食直补资源无法发挥相应的作用;另一方面,政府部门为了降低行政成本,往往选取往年的数据,从而导致粮食直补的资金被锁定,即粮食生产规模和面积与粮食直补脱钩,粮食直补无法实现“物尽其用”。总之,粮食直补并没有发挥相应的激励作用,反而给财政资源带来了极大的浪费,这样不仅不利于推进农业种植规模的扩大,而且容易导致“黑匣子”操作。
控制变量中,第一产业占比没有通过显著性检验,但对粮食作物播种面积的影响为负,即第一产业占GDP的比重越大,粮食作物播种面积就越小。人均常用耕地面积也没有通过显著性检验,但对粮食作物播种面积的影响为正,即人均常用耕地面积越大,粮食作物播种面积就越大。亩均农业机械动力在模型(1)中没有通过显著性检验,但在模型(2)中10%的水平上显著,且对粮食作物播种面积均有正影响。
在剩下的三个控制变量中,农业从业人员占比、粮食价格和有效灌溉耕地面积占比均通过显著性检验。农业从业人员占比在1%水平上负显著,即在模型(1)中,农业从业人员占比每提高1个百分点,粮食作物播种面积占比将减少0.773 6个百分点;在模型(2)中,农业从业人员占比每提高1个百分点,粮食作物播种面积占比将减少0.794 2个百分点。粮食价格在1%水平上正显著,即在模型(1)中,粮食价格每千克提高1元,粮食作物播种面积占比将增加1.368 7个百分点;在模型(2)中,粮食价格每千克提高1元,粮食作物播种面积占比将增加1.410 1个百分点。有效灌溉耕地面积占比也通过了显著性检验,但是,在模型(1)中,有效灌溉耕地面积占比在10%水平上负显著,即有效灌溉耕地面积占比每提高1个百分点,粮食作物播种面积占比将减少0.052 9个百分点;在模型(2)中,有效灌溉耕地面积占比在5%水平上负显著,即有效灌溉耕地面积占比每提高1个百分点,粮食作物播种面积占比将减少0.052 4个百分点。
为了更加全面、准确地分析不同区域粮食直补对粮食作物播种面积的影响,我们依据湖北省不同区域的农业发展状况,将其分为粮食主产区和非粮食主产区。分区域看,在粮食主产区和非粮食主产区的固定效应模型也与前文分析结果一致。在粮食主产区粮食直接补贴的估计系数为正,表明随着粮食补贴资金的增加,播种面积将增加。但在非粮食主产区,每亩粮食直补的估计系数为负。
具体的效应机制可能是,一方面,随着我国城镇化、工业化的推进和发展,地方政府更加注重第二、第三产业的发展,从而导致更多的劳动力、资金从农业向工业、服务业转移;再加上粮食直补分摊到每户种粮农民手上的金额不多,由于种粮机会成本太高,往往被看作对年迈劳动力的“养老金”,对年轻劳动力也没有吸引和激励机制。另一方面,生产粮食并不是非粮食主产区的支柱产业,粮食的生产和发展在一定程度上不能够适应当地的地理特征和气候特点,如果执意过度开发粮食耕地,很有可能导致滑坡、泥石流等自然灾害发生,不利于当地生态的可持续发展,反而会人为地增加自然灾害发生的可能性,因此在客观上粮食直补无法促进粮食播种规模的扩大。但值得注意的是,无论在粮食主产区还是在非粮食主产区,都没有通过显著性检验,粮食直接补贴对粮食作物播种面积的影响非常小,几乎接近为0,即无论粮食主产区还是非粮食主产区,粮食直接补贴对粮食作物播种面积都无影响。
此外,非粮食主产区的农业从业人员占比对粮食作物播种面积的负影响明显大于对粮食主产区的农业从业人员占比负影响;亩均农业机械动力对非粮食主产区的粮食作物播种面积的正影响也远大于对粮食主产区的正影响。
2)稳健性检验
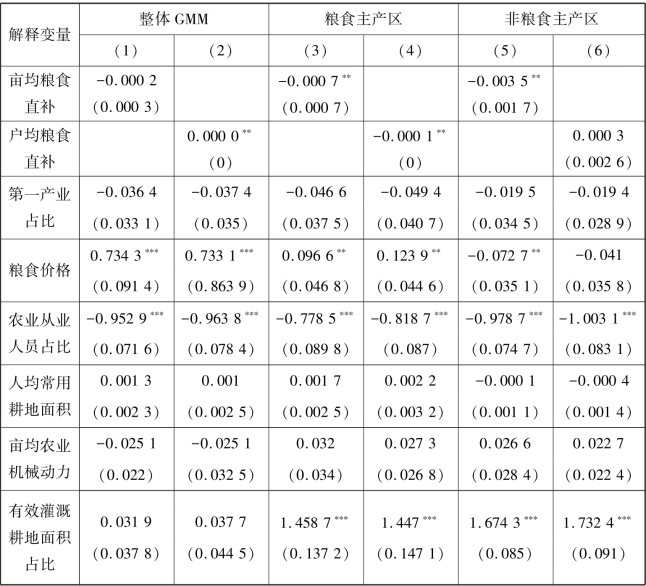
为进一步验证上述结果具有稳健性,我们在多元回归模型中引入粮食作物播种面积一阶滞后项,构建一个动态面板数据模型。本章采用系统广义矩估计方法对其进行估计,同时对估计结果进行Sargen检验,以验证工具变量的有效性,并对残差项是否存在一阶和二阶序列自相关进行了检验。系统广义矩估计具体可分为一步法和两步法。与一步法相比,两步法不易受到异方差的干扰,但两步法的标准误差在有限样本条件下可能产生向下偏倚。为此,本章遵循Windmeijer(2005)的方法对两步法标准差的偏差进行校正。表4.5给出的系统广义矩估计结果与固定效应模型中解释变量的符号和显著性基本一致,表明本书结论对不同的计量回归方法都是稳健的。从检验结果上看,AR(1)检验的P值均小于0.1,表明残差项存在显著的一阶自相关,而AR(2)检验的P值均大于0.5,表明残差项不存在二阶自相关,符合模型的设定条件;Sargen检验的P值均大于0.1,说明残差项与解释变量不相关,工具变量是合理的。另外,表4.5中粮食作物播种面积一阶滞后项的估计结果表明,粮食作物播种面积存在显著的持续性特征,故而上述结果再次证实了本章实证结果具备稳健性。
表4.5 粮食直接补贴对粮食作物播种面积影响的稳健性检验结果
续表
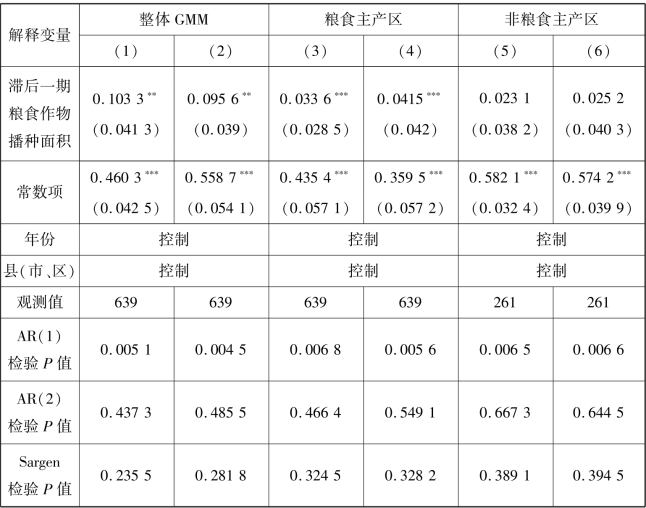
注:*,**和***分别表示在10%、5%和1%的水平上显著;括号内数字为标准差。
