参考文献
Gescheider,G.A.(1997).Psychophysics:The fundamentals(3rd ed.).Hillsdale,NJ:Lawrence Erlbaum Associates.
Laming,D.(1995).Psychophysics.In R.L.Gregory,& A.M.Colman(Eds),Sensation and perception(pp.97-123),London & New York:Longman.
※ ※ ※
8.(g,k)。一个得分点是,认识到还需要点燃7只蜡烛。另一个得分点是认为在香肠B中所加的盐量少于半勺。获得奖励分是能够正确地阐述幂定律。或者能够陈述费希纳定律(Fechner's law)就加0.5分。这两个定律我都将进行解释。问题8是一个非常令人困惑的问题,即使是感知觉方面的心理学专家,假如手头上没有通过实验而得到的准确数字,也很难完全正确地回答出这个问题。
就像问题7一样,在这个问题中,我们主要集中于产生该现象的心理感觉和物理刺激之间的关系。因此,这个研究领域被称为心理物理学(psychophysics),它是实验心理学中最古老的一个分支。心理物理学的中心问题可以用非常简单的方式描述:感觉量和刺激的强度是如何相关的?就像下面的想象实验所显示的,这个关系非常复杂。想象进入一个漆黑的房间,打开一盏100瓦的灯,然后再打开另一盏100瓦的灯。当第二盏灯被打开时,光的物理强度是原来的两倍,但是房间的亮度看起来并不是原来的两倍。与只有一盏灯时相比,实际上看起来只是稍微亮一点点。在这个例子中,至少可以表明感觉强度和刺激强度之间的关系并不是简单或显而易见的。
清楚理解此问题的第一人是德国哲学家、神秘主义者费希纳(Gustav Theodor Fechner,1801—1887)。费希纳是心理学历史上最富色彩的人物之一。他早期的一些著作主要是对天使们进行解剖比较分析,并证明月亮是由碘构成的。1850年10月22日的早晨,在费希纳准备起床之前,就像启示一般,他的大脑里突然闪现一种非常有用的观点。这就是感觉量上的相同增加伴随着刺激强度相同比率量的增加。换句话说,随着刺激的物理强度以相同的比率增加时,感觉量也会以相同的量增加。例如,依据这一规律,把物理强度从100瓦增加到200瓦所引起的光增量感,与把物理强度从200瓦增加到400瓦所引起的光增量感是相同的。同样,把物理的光照从60瓦增加到180瓦所产生的光增量感,与从100瓦增加到300瓦所引起的光增量感是相同的。原因是在每一种情况下,刺激的物理强度(以瓦特表示)是以相同的比率增加的:在第一个例子中,每一次是以两倍的形式增加;在第二个例子中,每一次是以三倍的形式增加。费希纳这一观点的最简单描述是:随着物理刺激量以相同的比率形式增加,感觉量以相同的等级形式增加。
费希纳认为他发现了解决哲学中心问题之一——即身心关系问题(见第5章)的方法。接下来,他花了10年的时间进行实验,来验证他的定律在各种感觉类型中的有效性。例如,从1855年到1859年,他既当实验者,又当被实验者,对自己进行了不少于67072次的重量比较实验。1860年,他出版了《心理物理学纲要》(Elements of Psychophysics)一书。在这本书里,他把心理物理学描述为“身心之间依存关系或功能关系的严密科学”。
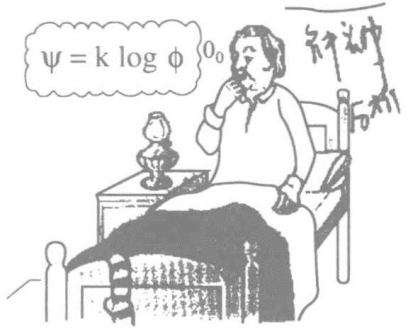
怎样采用数学的方式来描述费希纳定律?任何熟悉对数的人都知道,一般对数1、2、3、4等等,与算术数10、100、1000、10000等相对应。随着算术数以相同的比率增加,对数也以相同的等级增加。或者更精确地说,算术数每增加10倍,对数增加1个单元。因此,费希纳认为“感觉和刺激量的增加关系,与对数和算术数之间的增加关系是相似的”。假如以希腊字母ψ(心理量的缩写)来表示感觉量,以希腊字母φ(物理量的缩写)来表示刺激的强度,费希纳定律就可以用下面的公式表示:
在这个公式中,k是一个常量,随着感觉类型的不同而变化。
在几乎一个世纪的时间里,心理学家们认为费希纳的对数定律是基本有效的。尽管在实验中,它的预测性有时不是十分准确。费希纳定律有许多实际的用途。最闻名的可能是响度的分贝制。1分贝相当于1/10贝。贝是响度的单位,它是以电话的发明者贝尔(Alexander Graham Bell)的名字命名的。采用费希纳定律,k=10,φ代表声音的物理强度,ψ表示分贝的水平。在分贝表中,谈话时的声音大约是60分贝。假如两个人同时说话,虽然声音的物理强度增加了一倍,但是声音的分贝仅从60增加到63。假如四个人同时说话,将增加到66分贝,等等。分贝表在广播和电话设计中被使用,而且在全世界,各国的法律都依据分贝表来规定工业和环境的噪音。
遗憾的是,费希纳定律并不是完全正确的。美国哈佛大学的心理学家斯蒂文森(S.Smith Stevens)在1953年和1957年发表了两篇非常有影响的文章。在这两篇文章里,他介绍了一种与费希纳定律略有区别的定律,能够更准确地进行预测。该定律被称为幂定律(power law)。在实验室里进行测验时,幂定律具有非常准确的预测性。根据费希纳的对数定律,感觉量上的相同增加伴随着刺激强度以相同比率增加。依据幂定律,感觉量上相同比率的增加伴随着刺激强度上相同比率的增加,这两种比率之间不一定要求相同。例如,不管何时声音的物理强度增加2.80倍时,响度的感觉量都增加一倍。斯蒂文森定律可以用数学公式表示为:
其中ψ表示感觉量;k是依据被测内容而定的一个常数;φ是刺激的强度;n是幂,对于某一类型的感觉来说,n是一个常数;对不同类型的感觉,n值是不同的。
已经通过实验确定了不同类型感觉的n值。对于某些类型的感觉,例如视亮度(n=0.33),幂是小于1的。在这些情况下,当刺激强度以某一比率增加时,感觉量以更小的比率增加。就像前面所讲的想象实验中,进入一个黑暗的房间先打开一盏灯,然后打开另一盏灯。在这种情况下,依据对数定律和幂定律会得到相似的结果。但是在幂指数很大的情况下,例如电刺激感觉(n=3.5)或咸淡感觉(n=1.4),当刺激强度以一定比率增加时,会导致感觉量上比率很大的增加。在这些情况下,幂定律能够给予更准确的预测。对于某些类型的知觉来说,费希纳定律是非常适用的;但是对于另一些类型的知觉来说,费希纳定律的预测效果就比幂定律低很多。
现在我们回到问题的第一部分,刺激的物理强度是一支蜡烛所发出的光,此时φ=1。由于通过很多实验已经得出视亮度的幂指数是0.33,所以n=0.33。当点燃一支蜡烛时,幂定律就表示为:
当有更多的蜡烛被点燃时(具体不确定),此时的亮度心理量增加了一倍。用数学公式表示:
此时,我们需要上面的两个方程联合起来求解φ。最简单的方法就是分别用方程2ψ=k(φ)0.33的左边除以方程ψ=k(1)0.33的左边,右边除以右边。结果就会得出方程2=(φ)0.33/(1)0.33,通过计算得出φ的近似值为8。这一结果的意思就是,需要点燃8只蜡烛所发出的光才会引起感觉量增加一倍。换句话说,就是还须另外再点燃7支蜡烛。
在问题的第2部分里,A香肠含有1/4勺的盐,B香肠所含有的盐量φ是未知的,B香肠的咸度感觉起来是A香肠的两倍。问题8中的顾客可能记得咸淡感觉的幂指数是大于1的,因此认识到B香肠所含盐量一定少于A香肠所含盐量的两倍。但是只知道这些还没有完全解决问题。还应该把所有的已知量(包括正确的幂指数n=1.4)分别代入到方程中去,那么我们就会得到:
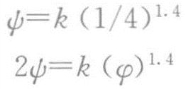
与上面的解法相同,两个方程的两边同时相除,就会得到:
通过计算可以得出φ=0.4。因此B香肠含有4/10或2/5勺的盐。假如你能正确地描述幂定律加1分,能够描述费希纳定律加0.5分。即使计算出B香肠所含有的确切盐量也不能再加分,但你可以自己给自己奖励10枚金星。
