统计：基本思想

人们通常很吃惊或者甚至沮丧地发现，统计在心理学中起着部分作用。而且就因为这个原因，有人放弃学习心理学的念头。事实上，心理学需要的数学能力是适度的，几乎没有人不能轻松掌握必须的技能。专业的心理学者们对统计的理解大不相同。大部分只是初步掌握基本的思想，就可以使他们使用一些简单的统计检验，尽管或多或少有些机械。他们相信，检验作了理应做的事。当遇到不能用常规或现有的方法解决的统计问题时，他们向更具统计头脑的同事寻求建议。

基本的统计知识对于理解心理学的专业文献是必不可少的。因为研究发现差不多总是以数字的形式呈现，而且要用统计的方法进行分析。统计有两大主要分支，叫做描述统计与推论统计。描述统计是以更容易说明问题的方式总结数据资料，包括用图、表呈现数据，计算平均分、方差、相关，等等。失业人数统计、商业统计与事故统计是描述统计众所周知的例子。自从19世纪60年代高尔顿将其用于智力（见第5章）的调查后，心理学一直使用描述统计法。另一方面，推论统计目的在于通过统计检验，从样本中做出推论来解释数据。统计检验使研究者可以决定，实验的结果存在统计意义上的显著性差异，还是仅仅偶然因素也能产生类似的结果。

推论统计的基本逻辑是迂回的、难捉摸的，但我想我能解释清楚。一个基本的例子可以弄清所有的问题。我准备从基本原理上逐渐揭示统计检验，阐明检验的基本思想。在前面的章节中，我概述了一个实验：探查哪种教学方法，口语的还是写作的，对孩子的外语学习更有效。让我们假设，理论或前人的研究说明口语训练比写作训练更有效，而一位研究者试图检验这一假设。为使问题简单化，实验者仅采用六名儿童作为被试，每组（口语训练与写作训练）随机分配三名。然后除了操纵自变量（教学方法）以外，实验者在其他方面的处理完全一致。整个程序可以在计算机与装备完善的语言实验室的帮助下自动操作，随后给每个孩子合适的测验测量因变量（外语知识）。还是为了简化的目的，假设测验根据每个孩子的外语知识水平，只给出他们的等级评定，从最差到最好。用字母O代表采用口语训练法教学的孩子，W代表写作训练的孩子，将六名被试的成绩按照从左至右，最差到最好的顺序排列，假设结果是这个样子的：

WWOWOO

表面看来口语训练法似乎效果更好，与假设一致。因为大部分口语训练法的孩子成绩等级高于大部分写作训练法的孩子。三个口语训练法的孩子分别是第一、第二和第四；而三个写作训练法的孩子分别是第三、第五和第六。当然，年龄、智力、动机等因素会影响结果。但我们知道这些额外变量在两组中是随机分布的，因为被试是随机分配至两组中的。

让我们将最差的等级（垫底的孩子）计作1，下一个等级计作2，等等，直到最高的等级6。我们想知道的是口语训练法得到的等级是否显著高于写作训练法的。口语训练法的孩子总的等级是：3+5+6=14，而写作训练法的孩子总的等级是：1+2+4=7。O被试比W被试高出的等级是14-7=7，因此我们说等级的差距是7。这是对口语法有利的差异。这个差异是否仅仅是由偶然因素造成？是的，我们不能驳斥差异是由偶然因素造成的可能性。但是，在这里由于我们使用了随机化，我们可以精确地计算出由偶然因素造成这样大的差距的概率是多少。

我们需要知道，仅仅由于偶然得到的等级之差在假设的方向上（对口语训练法有利），至少与实际所得差距相同的概率是多少。三个O与三个W的等级排列有20种不同的方式。为了理解得更清楚，想象顺序排列三个红球与三个白球，你会发现不同的组合方式只有20种可能的形式。如果每一个元素都是随机改变位置，那么每一种排列方式的可能性是等同的。下面是全部的清单，包括等级之差（O等级之和减去W等级之和）：

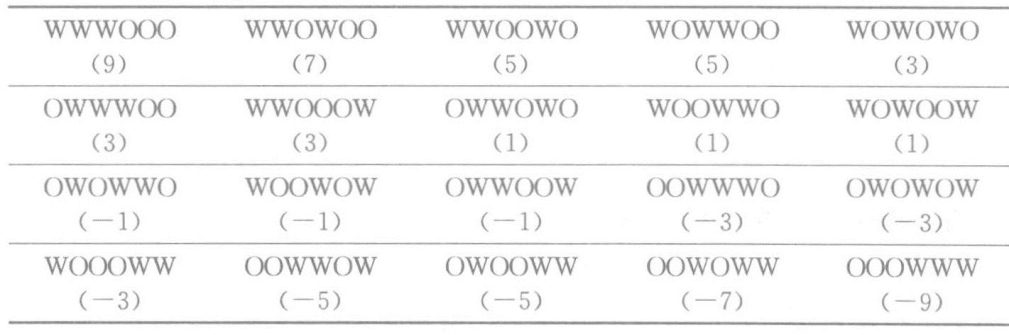
从表中明显可见，在20种可能性等同的排列中，只有两个（最上面一行的前两个）在假设方向上至少与实际所得结果有相同差距；剩下所有的等级之差都小一些。仅凭偶然所得与实验所得结果至少具有相同差距的概率是2/20，或10％。这意味着，如果自变量（不同的教学方法）对因变量压根没有任何影响，而且如果实验重复很多次，凭偶然约有10％的实验结果在对口语训练法有利的方向上与实际所得结果差距相同。换言之，结果不能使我们非常有把握地作出结论，是实验中的教学方法造成了差异。按照惯例，假如偶然的概率小于5％，那么心理学家通常把实验结果称作统计意义上具有显著性。事实上对如此少的被试，在0.05的显著性水平上，唯一的排列是WWWOOO，它代表所有同等可能性的结果中5％（1/20）的概率。

我刚才描述的是曼—惠特尼U检验。当样本更大时，研究者不会像我那样费力地列出所有等同概率的结果，然后进行统计。因为当样本容量增加时，结果的数量会变得非常大。研究者只是运用一些计算公式，然后查表求显著性水平的值。大多数心理学研究的结果是由一些少数的统计检验公式分析的。这些公式功能强大且有效，而且使用非常容易。所有这些检验的逻辑在本质上是相同的。每一个统计显著性检验都是假设自变量没有任何效应，因变量的变化是偶然因素造成的，这就是所谓的零假设。备择假设或实验假设是实验者的假设：一些特定的差异是由自变量造成的。检验时计算仅凭偶然得到的差异至少与实际所得差异一样的概率，这个概率叫做显著性水平（significance level）。如果显著性水平足够小，通常小于5％，那么实验者就可以拒绝零假设而将结果归因于备择假设。如果实验得到充分控制，那么除偶然因素之外，备择假设是唯一可能的解释。另一方面，如果显著性水平不够小，就不能做出确定的结论，结果往往被称作不显著。

这就是零假设检验的逻辑。零假设的重要性源于判断研究数据的显著性需要客观的标准。这增加了可由数学结果推论而出的结论的重要性，下面的例子将展示这一点。