(试卷Ⅳ)
一、判断题(本题共5小题,每小题2分,满分10分)
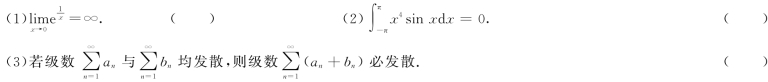
(4)假设D是矩阵A的r阶子式,且D≠0,但含D的一切r+1阶子式都等于0,那么矩阵A的一切r+1阶子式都等于0.( )
(5)连续型随机变量取任何给定实数值的概率等于0.( )
二、选择题(本题共5小题,每小题2分,满分10分)
(1)下列函数在其定义域内连续的是
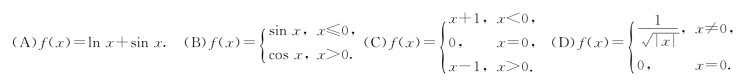
(2)若f(x)在(a,b)内可导且a<x1<x2<b,则至少存在一点ξ,使得
(A)f(b)-f(a)=f′(ξ)(b-a)(a<ξ<b).
(B)f(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b).
(C)f(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2).
(D)f(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2).
(3)下列广义积分收敛的是
![]()
(4)设n阶方阵A的秩r(A)=r<n,那么在A的n个行向量中
(A)必有r个行向量线性无关.
(B)任意r个行向量都线性无关.
(C)任意r个行向量都构成极大线性无关向量组.
(D)任意一个行向量都可以由其他r个行向量线性表示.
(5)若两事件A和B同时出现的概率P(AB)=0,则
(A)A和B不相容(互斥).(B)AB是不可能事件.
(C)AB未必是不可能事件.(D)P(A)=0或P(B)=0.
三、(本题共4小题,每小题4分,满分16分)
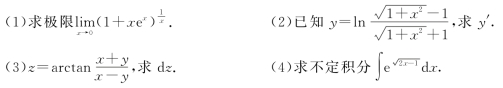 (https://www.daowen.com)
(https://www.daowen.com)
四、(本题满分10分)
考虑函数![]() 问:
问:
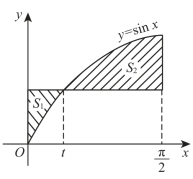
(1)t取何值时,右图中阴影部分的面积S1与S2之和S=S1+S2最小?
(2)t取何值时,面积S=S1+S2最大?
五、(本题满分6分)
将函数![]() 展开成x的幂级数,并指出收敛区间.
展开成x的幂级数,并指出收敛区间.
六、(本题满分5分)
计算二重积分![]() ,其中D是第一象限中由直线y=x和曲线y=x3围成的封闭区域.
,其中D是第一象限中由直线y=x和曲线y=x3围成的封闭区域.
七、(本题满分6分)
已知某商品的需求量x对价格p的弹性η=-3p3,而市场对该商品的最大需求量为1(万件).求需求函数.
八、(本题满分8分)
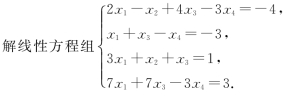
九、(本题满分7分)
设矩阵A和B满足AB=A+2B,求矩阵B,其中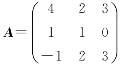 .
.
十、(本题满分6分)
求矩阵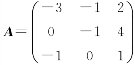 的实特征值及对应的特征向量.
的实特征值及对应的特征向量.
十一、(本题共2小题,每小题4分,满分8分)
(1)已知随机变量X的概率分布为P{X=1}=0.2,P{X=2}=0.3,P{X=3}=0.5,试写出X的分布函数F
(2)已知随机变量Y的概率密度为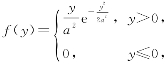 求随机变量
求随机变量![]() 的数学期望EZ.
的数学期望EZ.
十二、(本题满分8分)
假设有两箱同种零件:第一箱内装50件,其中10件一等品;第二箱内装30件,其中18件一等品,现从两箱挑出一箱,然后从该箱中先后随机取两个零件(取出的零件均不放回).试求:
(1)先取出的零件是一等品的概率p;
(2)在先取出的零件是一等品的条件下,第二次取出的零件仍然是一等品的条件概率q.
