（试卷Ⅳ）
一、填空题（本题共5小题，每小题3分，满分15分）
（1）设z＝esin xy，则d z＝_________.
（2）设曲线f（x）＝x 3＋ax与g（x）＝bx 2＋c都通过点（－1，0），且在点（－1，0）有公共切线，则a＝_________，b＝_________，c＝_______.
（3）设f（x）＝x e x，则f（n）（x）在点x＝_______处取极小值_______.
（4）设A和B为可逆矩阵，
为分块矩阵，则X－1＝_________.
（5）设随机变量X的分布函数为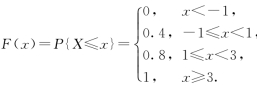
则X的概率分布为_______.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）下列各式中正确的是
（3）设A为n阶可逆矩阵，λ是A的一个特征值，则A的伴随矩阵A*的特征值之一是
(A)λ－1|A|n.(B)λ－1|A|.(C)λ|A|.(D)λ|A|n.
（4）设A和B是任意两个概率不为零的互不相容事件，则下列结论中肯定正确的是
（5）对任意两个随机变量X和Y，若E（XY）＝EXEY，则
（A）D（XY）＝DXDY.（B）D（X＋Y）＝DX＋DY.（C）X与Y独立．（D）X与Y不独立．
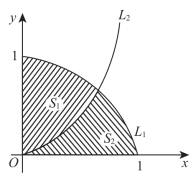
六、（本题满分5分）假设曲线L 1：y＝1－x 2（0≤x≤1），x轴和y轴所围区域被曲线L 2：y＝ax 2分为面积相等的两部分（如图），其中a是大于零的常数，试确定a的值．
七、（本题满分8分）
某厂家生产的一种产品同时在两个市场销售，售价分别为p 1和p 2，销售量分别为q 1和q 2，需求函数分别为q 1＝24－0.2p 1和q 2＝10－0.05p 2，总成本函数为C＝35＋40（q1＋q2）.试问：厂家如何确定两个市场的售价，能使其获得的总利润最大？最大总利润为多少？
八、（本题满分6分）试证明函数
在区间（0，＋∞）内单调增加．
九、（本题满分7分）
设有3维列向量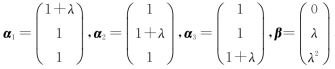
，问λ取何值时：
（1）β可由α1，α2，α3线性表示，且表达式唯一？（2）β可由α1，α2，α3线性表示，但表达式不唯一？
（3）β不能由α1，α2，α3线性表示？
十、（本题满分6分）考虑二次型
，问λ取何值时，f为正定二次型？
十一、（本题满分6分）
十二、（本题满分6分）【同试卷Ⅴ 第十三、（1）题】
十三、（本题满分6分）假设随机变量X和Y在圆域x 2＋y 2≤r 2上服从联合均匀分布．
（1）求X和Y的相关系数ρ；（2）问X和Y是否独立？
十四、（本题满分5分）
设总体X的概率密度为
其中λ＞0是未知参数，a＞0是已知常数．试根据来自总体X的简单随机样本X 1，X 2，…，X n，求λ的最大似然估计量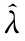
.