（试卷Ⅳ）
一、填空题（本题共4小题，每小题3分，满分12分）
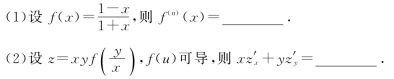
（3）设f′（ln x）＝1＋x，则f（x）＝_________.
（4）设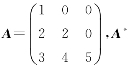
是A的伴随矩阵，则（A*）－1＝_________.
二、选择题（本题共5小题，每小题3分，满分15分）
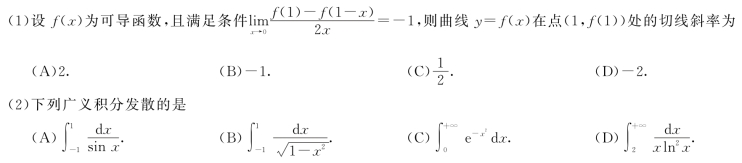
（3）设矩阵A m×n的秩为r（A）＝m＜n，E m为m阶单位矩阵，则下述结论中正确的是
（A）A的任意m个列向量必线性无关．（B）A的任意一个m阶子式不等于零．
（C）若矩阵B满足BA＝O，则B＝O.（D）A通过初等行变换，必可以化为（E m O）的形式．
（4）设随机变量X和Y独立同分布，记U＝X－Y，V＝X＋Y，则随机变量U与V必然
（A）不独立．（B）独立．（C）相关系数不为零．（D）相关系数为零．
（5）设随机变量X～N（μ，σ2），则随着σ的增大，概率P{|X－μ|＜σ}
（A）单调增大．（B）单调减小．（C）保持不变．（D）增减不定．
三、（本题满分6分）
设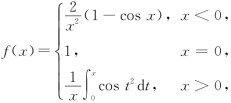
讨论f（x）在x＝0处的连续性和可导性．
四、（本题满分6分）
已知连续函数f（x）满足条件
，求f（x）．
五、（本题满分6分）
将函数y＝ln（1－x－2x 2）展开成x的幂级数，并指出其收敛区间．
六、（本题满分6分）
计算二次积分
．
七、（本题满分6分）
设某产品的需求函数为Q＝Q（P），收益函数为R＝PQ，其中P为产品价格，Q为需求量（产品的产量），Q（P）是单调减函数，如果当价格为P 0，对应产量为Q 0时，边际收益
，收益对价格的边际效应
，需求对价格的弹性为E P＝b＞1，求P 0和Q 0．
八、（本题满分8分）
设f（x），g（x）在区间[－a，a]（a＞0）上连续，g（x）为偶函数，且f（x）满足条件f（x）＋f（－x）＝A（A为常数）．
（1）证明
（2）利用（1）的结论计算定积分
．
九、（本题满分9分）
已知向量组（Ⅰ）α1，α2，α3；（Ⅱ）α1，α2，α3，α4；（Ⅲ）α1，α2，α3，α5．如果各向量组的秩分别为r（Ⅰ）＝r（Ⅱ）＝3，r（Ⅲ）＝4．证明：向量组α1，α2，α3，α5－α4的秩为4．
十、（本题满分10分）
已知二次型f（x 1，x 2，x 3）＝4x 22－3x 23＋4x 1 x 2－4x 1 x 3＋8x 2 x 3.
（1）写出二次型f的矩阵表达式；
（2）用正交变换把二次型f化为标准形，并写出相应的正交矩阵．
十一、（本题满分8分）
假设一厂家生产的每台仪器，以概率0.70可以直接出厂；以概率0.30需进一步调试，经调试后以概率0.80可以出厂；以概率0.20定为不合格品不能出厂，现该厂生产了n（n≥2）台仪器（假设各台仪器的生产过程相互独立）.求（1）全部能出厂的概率α；（2）其中恰好有两台不能出厂的概率β；（3）其中至少有两台不能出厂的概率θ.
十二、（本题满分8分）
已知随机变量X和Y的联合概率密度为
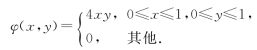
求X和Y的联合分布F（x，y）.