2022年全国硕士研究生招生考试数学三试题
姓名_______分数_______
一、选择题：1～10小题，每小题5分，共50分.下列每题给出的四个选项中，只有一个选项是最符合题目要求的.
1．当x→0时，α（x），β（x）是非零无穷小量，给出以下四个命题：
①若α（x）～β（x），则α2（x）～β2（x）；
②若α2（x）～β2（x），则α（x）～β（x）；
③若α（x）～β（x），则α（x）－β（x）＝o（α（x））；
④若α（x）－β（x）＝o（α（x）），则α（x）～β（x）．
其中所有真命题的序号是
A．①③．B．①④．
C．②③④．D．①③④．
2．已知，则{an}
A．有最大值，没有最小值．B．有最大值，有最小值．
C．没有最大值，有最小值．D．没有最大值，没有最小值．
A．存在可逆矩阵P，Q，使得A＝PΛQ．
B．存在可逆矩阵P，使得A＝PΛP－1．
C．存在正交矩阵Q，使得A＝QΛQ－1．
D．存在可逆矩阵P，使得A＝PΛPT．
6．设矩阵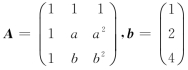
，则线性方程组Ax＝b解的情况为
A．无解．B．有解．
C．有无穷多解或无解．D．有唯一解或无解．
10．设二维随机变量（X，Y）的概率分布为
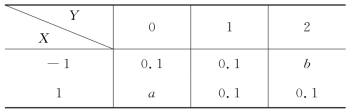
若事件{max{X，Y}＝2}与事件{min{X，Y}＝1}相互独立，则Cov（X，Y）＝
A．－0．6．B．－0．36．C．0．D．0．48．
二、填空题：11～16小题，每小题5分，共30分.
三、解答题：17～22小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（本题满分10分）
设函数y（x）是微分方程
满足条件y（1）＝3的解，求曲线y＝y（x）的渐近线．
18．（本题满分12分）
设某产品的产量Q由资本投入量x和劳动投入量y决定，生产函数为
，该产品的销售单价p与Q的关系为p＝1160－1．5Q．若单位资本投入和单位劳动投入的价格分别为6和8，求利润最大时的产量．
22．（本题满分12分）设X1，X2，…，Xn为来自均值为θ的指数分布总体的简单随机样本，Y1，Y2，…，Ym为来自均值为2θ的指数分布总体的简单随机样本，且两样本相互独立，其中θ（θ＞0）是未知参数．利用样本X1，X2，…，Xn，Y1，Y2，…，Ym，求θ的最大似然估计量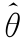
，并求D（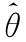
）．