2001年全国硕士研究生入学统一考试数学三试题
姓名_______分数_______
一、填空题：1～5小题，每小题3分，共15分．
（1）设生产函数为Q＝ALαKβ，其中Q是产出量，L是劳动投入量，K是资本投入量，而A，α，β均为大于零的参数，则当Q＝1时K关于L的弹性为_________．
（2）某公司每年的工资总额在比上一年增加20%的基础上再追加2百万元．若以Wt表示第t年的工资总额（单位：百万元），则Wt满足的差分方程是_________．
（3）设矩阵
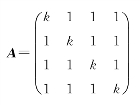
且r（A）＝3，则k＝_________．
（4）设随机变量X和Y的数学期望分别为－2和2，方差分别为1和4，而相关系数为－0.5，则根据切比雪夫不等式P{|X＋Y|≥6}≤___________．
（5）设总体X服从正态分布N（0，22），而X1，X2，…，X15是来自总体X的简单随机样本，则随机变量
服从_________分布，参数为_________．
二、选择题：6～10小题，每小题3分，共15分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（6）设f（x）的导数在x＝a处连续，又
，则
（A）x＝a是f（x）的极小值点．
（B）x＝a是f（x）的极大值点．
（C）（a，f（a））是曲线y＝f（x）的拐点．
（D）x＝a不是f（x）的极值点，（a，f（a））也不是曲线y＝f（x）的拐点．
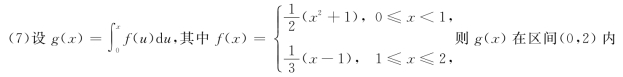
（A）无界．（B）递减．（C）不连续．（D）连续．
（8）设
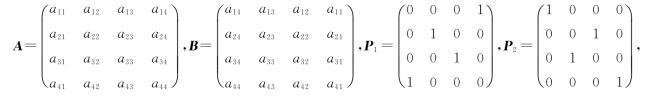
其中A可逆，则B－1等于
(A)A－1P1P2．(B)P1A－1P2．(C)P1P2A－1．(D)P2A－1P1．
（9）设A是n阶矩阵，α是n维列向量．若
，则线性方程组
（10）将一枚硬币重复掷n次，以X和Y分别表示正面向上和反面向上的次数，则X和Y的相关系数等于
(A)－1．(B)0．(C)
．(D)1．
三、解答题：11～20小题，共70分．解答应写出文字说明、证明过程或演算步骤．
（11）（本题满分5分）
设u＝f（x，y，z）有连续的一阶偏导数，又函数y＝y（x）及z＝z（x）分别由下列两式确定：
（12）（本题满分6分）
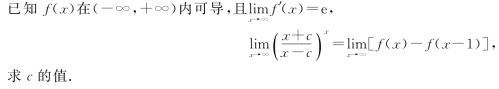
（13）（本题满分6分）
求二重积分
的值，其中D是由直线y＝x，y＝－1及x＝1围成的平面区域．
（14）（本题满分7分）
已知抛物线y＝px2＋qx（其中p＜0，q＞0）在第一象限内与直线x＋y＝5相切，且此抛物线与x轴所围成的平面图形的面积为S．
（Ⅰ）问p和q为何值时，S达到最大值？
（Ⅱ）求出此最大值．
（17）（本题满分9分）
设矩阵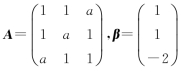
．已知线性方程组AX＝β有解但不唯一，试求
（Ⅰ）a的值；
（Ⅱ）正交矩阵Q，使QTAQ为对角矩阵．
（18）（本题满分8分）
设A为n阶实对称矩阵，r（A）＝n，Aij是A＝（aij）n×n中元素aij的代数余子式（i，j＝1，2，…，n），二次型
（Ⅰ）记X＝（x1，x2，…，xn）T，把f（x1，x2，…，xn）写成矩阵形式，并证明二次型f（X）的矩阵为A－1；
（Ⅱ）二次型g（X）＝XTAX与f（X）的规范形是否相同？说明理由．
（19）（本题满分8分）
一生产线生产的产品成箱包装，每箱的重量是随机的．假设每箱平均重50千克，标准差为5千克．若用最大载重量为5吨的汽车承运，试利用中心极限定理说明每辆车最多可以装多少箱，才能保障不超载的概率大于0.977．（Φ（2）＝0.977，其中Φ（x）是标准正态分布函数）
（20）（本题满分8分）
设随机变量X和Y的联合分布是正方形G＝{（x，y）|1≤x≤3，1≤y≤3}上的均匀分布，试求随机变量U＝
的概率密度p（u）．