（试卷Ⅴ）
一、填空题（本题共5小题，每小题3分，满分15分）
（1）【同试卷Ⅳ 第一、（1）题】 （2）【同试卷Ⅳ 第一、（2）题】 （3）【同试卷Ⅳ 第一、（3）题】
（5）设A，B为随机事件，P（A）＝0.7，P（A－B）＝0.3，则P（AB）＝_________.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）【同试卷Ⅳ 第二、（1）题】
（2）设数列的通项为：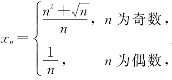
则当n→∞，x n是
（A）无穷大量．（B）无穷小量．（C）有界变量．（D）无界变量．
（3）设A与B为n阶方阵，且AB＝O，则必有
（A）A＝O或B＝O.（B）AB＝BA.（C）|A|＝0或|B|＝0.（D）|A|＋|B|＝0.
（4）设A是m×n矩阵，Ax＝0是非齐次线性方程组Ax＝b所对应的齐次线性方程组，则下列结论正确的是
（A）若Ax＝0仅有零解，则Ax＝b有唯一解．（B）若Ax＝0有非零解，则Ax＝b有无穷多个解．
（C）若Ax＝b有无穷多个解，则Ax＝0仅有零解．（D）若Ax＝b有无穷多个解，则Ax＝0有非零解．
（5）【同试卷Ⅳ 第二、（4）题】
六、（本题满分5分）
已知xy＝xf（z）＋yg（z），xf′（z）＋yg′（z）≠0，其中z＝z（x，y）是x和y的函数，求证
七、（本题满分6分）【同试卷Ⅳ 第六题】 八、（本题满分8分）【同试卷Ⅳ 第七题】
九、（本题满分6分）证明不等式
.
十、（本题满分5分）
设n阶矩阵A和B满足条件A＋B＝AB．
（1）证明A－E为可逆矩阵；（2）已知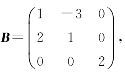
求矩阵A．
十一、（本题满分7分）【同试卷Ⅳ 第九题】
十二、（本题满分5分）
已知向量α＝（1，k，1）T是矩阵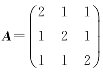
的逆矩阵A－1的特征向量，试求常数k的值．
十三、（本题满分7分）
一汽车沿一街道行驶，需要通过三个均设有红绿信号灯的路口，每个信号灯为红或绿与其他信号灯为红或绿相互独立，且红绿两种信号显示的时间相等．以X表示该汽车首次遇到红灯前已通过的路口的个数．
（1）求X的概率分布；（2）求
.
十四、（本题满分6分）
在电源电压不超过200伏，200～240伏和超过240伏三种情况下，某种电子元件损坏的概率分别为0.1，0.001和0.2.假设电源电压X服从正态分布N（220，252）.试求：
（1）该电子元件损坏的概率α；（2）该电子元件损坏时，电源电压在200～240伏的概率β.
[附表]（表中Φ（x）是标准正态分布函数）
