（试卷Ⅴ）
一、填空题（本题共5小题，每小题3分，满分15分）
（2）【同试卷Ⅳ 第一、（1）题】
（3）设f（x）＝sin x，f[φ（x）]＝1－x 2，则φ（x）＝_________；其定义域为_______.
（4）矩阵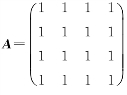
的非零特征值是_______.
（5）设对于事件A，B，C，有
，则A，B，C三个事件中至少出现一个的概率为_______.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）【同试卷Ⅳ 第二、（1）题】
（2）当x→0时，下列四个无穷小量中，比其他三个更高阶的无穷小量是
(A)x 2.(B)1－cos x.(C)
(D)x－sin x.
（3）设A，B，A＋B，A－1＋B－1均为n阶可逆矩阵，则（A－1＋B－1）－1等于
(A)A－1＋B－1.(B)A＋B.(C)A(A＋B)－1B.(D)(A＋B)－1.
（4）设α1，α2，…，αm均为n维向量，那么下列结论正确的是
（A）若k 1α1＋k 2α2＋…＋k mαm＝0，则α1，α2，…，αm线性相关．
（B）若对任意一组不全为零的数k 1，k 2，…，k m，都有k 1α1＋k 2α2＋…＋k mαm≠0，则α1，α2，…，αm线性无关．
（C）若α1，α2，…，αm线性相关，则对任意一组不全为零的数k 1，k2，…，km，都有k 1α1＋k 2α2＋…＋kmαm＝0．
（D）若0α1＋0α2＋…＋0αm＝0，则α1，α2，…，αm线性无关．
（5）【同试卷Ⅳ 第二、（4）题】
三、（本题满分5分）求极限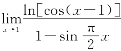
．
四、（本题满分5分）【同试卷Ⅳ 第四题】
五、（本题满分6分）求连续函数f（x），使它满足
．
六、（本题满分5分）【同试卷Ⅳ 第五题】
七、（本题满分6分）
设生产某产品的固定成本为10，而当产量为x时的边际成本函数为MC＝－40－20x＋3x 2，边际收入函数为MR＝32＋10x.试求：
（1）总利润函数；（2）使总利润最大的产量．
八、（本题满分6分）求证：方程x＋p＋q cos x＝0恰有一个实根，其中p，q为常数，且0＜q＜1．
九、（本题满分7分）给定曲线
.
（1）求曲线在横坐标为x 0的点处的切线方程；（2）求曲线的切线被两坐标轴所截线段的最短长度．
十、（本题满分5分）
设矩阵X满足AX＋E＝A 2＋X，其中E为3阶单位阵，又已知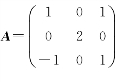
，试求出矩阵X.
十一、（本题满分5分）
设线性方程组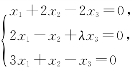
的系数矩阵为A，3阶矩阵B≠O，且AB＝O.试求λ的值．
十二、（本题满分6分）
已知实矩阵A＝（aij）3×3满足条件：①aij＝A ij（i，j＝1，2，3），其中A ij是a ij的代数余子式；②a 11≠0．计算行列式|A|．
十三、（本题满分7分）【同试卷Ⅳ 第十二题】 十四、（本题满分7分）【同试卷Ⅳ 第十三题】