（试卷Ⅳ）
一、填空题（本题共4小题，每小题3分，满分12分）
（1）设方程x＝yy确定y是x的函数，则dy＝_________.
（3）设（x0，y0）是抛物线y＝ax2＋bx＋c上的一点．若在该点的切线过原点，则系数应满足的关系是_______.
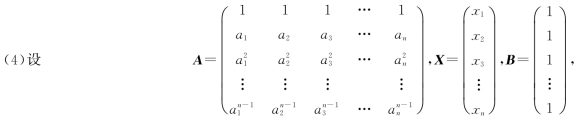
其中ai≠aj（i≠j；i，j＝1，2，…，n）．则线性方程组ATX＝B的解是_______.
二、选择题（本题共5小题，每小题3分，满分15分）
（3）设n阶矩阵A非奇异（n≥2），A*是矩阵A的伴随矩阵，则
(A)(A*)*＝|A|n－1A.(B)(A*)*＝|A|n＋1A.(C)(A*)*＝|A|n－2A.(D)(A*)*＝|A|n＋2A.
（4）设有任意两个n维向量组α1，…，αm和β1，…，βm，若存在两组不全为零的数λ1，…，λm和k1，…，km，使（λ1＋k1）α1＋…＋（λm＋km）αm＋（λ1－k1）β1＋…＋（λm－km）βm＝0，则
（A）α1，…，αm和β1，…，βm都线性相关．（B）α1，…，αm和β1，…，βm都线性无关．
（C）α1＋β1，…，αm＋βm，α1－β1，…，αm－βm线性无关．（D）α1＋β1，…，αm＋βm，α1－β1，…，αm－βm线性相关．
（5）已知0＜P（B）＜1，且P[（A1＋A2）|B]＝P（A1|B）＋P（A2|B），则下列选项成立的是
三、（本题满分6分）设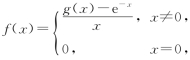
其中g（x）有二阶连续导数，且g（0）＝1，g′（0）＝－1．
（1）求f′（x）；（2）讨论f′（x）在（－∞，＋∞）上的连续性．
（1）求p在何范围变化时，使相应销售额增加或减少；（2）要使销售额最大，商品单价p应取何值？最大销售额是多少？
（1）已知A的一个特征值为3，试求y；（2）求矩阵P，使（AP）T（AP）为对角矩阵．
十、（本题满分8分）设向量组α1，α2，…，αt是齐次线性方程组Ax＝0的一个基础解系，向量β不是方程组Ax＝0的解，即Aβ≠0．试证明：向量组β，β＋α1，β＋α2，…，β＋αt线性无关．
十一、（本题满分7分）假设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作．若一周5个工作日里无故障，可获利润10万元；发生一次故障仍可获利润5万元；发生二次故障所获利润0元；发生三次或三次以上故障就要亏损2万元，求一周内利润的期望是多少？
十二、（本题满分6分）考虑一元二次方程x2＋Bx＋C＝0，其中B，C分别是将一枚色子（骰子）接连掷两次先后出现的点数，求该方程有实根的概率p和有重根的概率q.
十三、（本题满分6分）假设X1，X2，…，Xn是来自总体X的简单随机样本，已知E（Xk）＝αk（k＝1，2，3，4）.证明：当n充分大时，随机变量
近似服从正态分布，并指出其分布参数．