2020年全国硕士研究生招生考试数学三试题
姓名_______分数_______
一、选择题：1～8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
A．bsina．B．bcosa．
C．bsinf(a)．D．bcosf(a)．
2.函数
的第二类间断点的个数为
A．1．B．2．C．3．D．4．
3.设奇函数f（x）在（－∞，＋∞）上具有连续导数，则
4.设幂级数
的收敛区间为（－2，6），则
的收敛区间为
A．(－2,6)．B．(－3,1)．C．(－5,3)．D．(－17,15)．
5.设4阶矩阵A＝（aij）不可逆，a12的代数余子式A12≠0，α1，α2，α3，α4为矩阵A的列向量组，A*为A的伴随矩阵，则方程组A*x＝0的通解为
A．x＝k1α1＋k2α2＋k3α3，其中k1，k2，k3为任意常数．
B．x＝k1α1＋k2α2＋k3α4，其中k1，k2，k3为任意常数．
C．x＝k1α1＋k2α3＋k3α4，其中k1，k2，k3为任意常数．
D．x＝k1α2＋k2α3＋k3α4，其中k1，k2，k3为任意常数．
6.设A为3阶矩阵，α1，α2为A的属于特征值1的线性无关的特征向量，α3为A的属于特征值－1的特征向量，则满足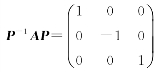
的可逆矩阵P可为
A．(α1＋α3,α2,－α3)．B．(α1＋α2,α2,－α3)．
C．(α1＋α3,－α3,α2)．D．(α1＋α2,－α3,α2)．
7.设A，B，C为三个随机事件，且
则A，B，C中恰有一个事件发生的概率为
8.设随机变量（X，Y）服从二维正态分布
，则下列随机变量中服从标准正态分布且与X独立的是
二、填空题：9～14小题，每小题4分，共24分．
三、解答题：15～23小题，共94分．解答应写出文字说明、证明过程或演算步骤．
15.（本题满分10分）
已知a，b为常数，若
在n→∞时是等价无穷小，求a，b．
16.（本题满分10分）
求函数f（x，y）＝x3＋8y3－xy的极值．
17.（本题满分10分）
设函数y＝f（x）满足y″＋2y′＋5y＝0，且f（0）＝1，f′（0）＝－1．
（1）求f（x）的表达式；
（2）设
．
18.（本题满分10分）
（1）存在ξ∈（0，2），使得|f′（ξ）|≥M；
（2）若对任意的x∈（0，2），|f′（x）|≤M，则M＝0．
20.（本题满分11分）
设二次型
经正交变换
化为二次型
，其中a≥b．
（1）求a，b的值；
（2）求正交矩阵Q．
21.（本题满分11分）
设A为2阶矩阵，P＝（α，Aα），其中α是非零向量且不是A的特征向量．
（1）证明P为可逆矩阵；
（2）若A2α＋Aα－6α＝0，求P－1AP，并判断A是否相似于对角矩阵．
22.（本题满分11分）
设二维随机变量（X，Y）在区域
上服从均匀分布，令
（1）求二维随机变量（Z1，Z2）的概率分布；
（2）求Z1与Z2的相关系数．
23.（本题满分11分）
设某种元件的使用寿命T的分布函数为
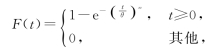
其中θ，m为参数且大于零．
（1）求概率P{T＞t}与P{T＞s＋t|T＞s}，其中s＞0，t＞0；
（2）任取n个这种元件做寿命试验，测得它们的寿命分别为t1，t2，…，tn．若m已知，求θ的最大似然估计值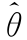
．