1998年全国硕士研究生入学统一考试数学三试题
姓名_______分数_______
一、填空题：1～5小题，每小题3分，共15分．
（1）设曲线f（x）＝xn在点（1，1）处的切线与x轴的交点为（ξn，0），则lni→m∞f（ξn）＝___________．
（3）差分方程2yt＋1＋10yt－5t＝0的通解为_________．
（4）设矩阵A，B满足A*BA＝2BA－8E，其中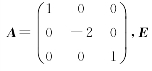
为单位矩阵，A*为A的伴随矩阵，则B＝___________．
（5）设X1，X2，X3，X4是来自正态总体N（0，22）的简单随机样本，
，其中a，b≠0．
则当a＝___________，b＝___________时，统计量X服从χ2分布，其自由度为_________．
二、选择题：6～10小题，每小题3分，共15分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（6）设周期函数f（x）在（－∞，＋∞）内可导，周期为4．
，则曲线y＝f（x）在点（5，f（5））处的切线的斜率为
（A）不存在间断点．（B）存在间断点x＝1．
（C）存在间断点x＝0．（D）存在间断点x＝－1．
（8）齐次线性方程组
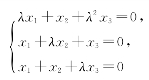
的系数矩阵记为A．若存在3阶矩阵B≠O使得AB＝O，则
（A）λ＝－2且|B|＝0．（B）λ＝－2且|B|≠0．
（C）λ＝1且|B|＝0．（D）λ＝1且|B|≠0．
（9）设n（n≥3）阶矩阵
若矩阵A的秩为n－1，则a必为
（10）设F1（x）与F2（x）分别为随机变量X1与X2的分布函数．为使F（x）＝aF1（x）－bF2（x）是某一随机变量的分布函数，在下列给定的各组数值中应取
三、解答题：11～20小题，共70分．解答应写出文字说明、证明过程或演算步骤．
（11）（本题满分5分）
（12）（本题满分5分）
（13）（本题满分6分）
设某酒厂有一批新酿的好酒，如果现在（假定t＝0）就售出，总收入为R0（元）．如果窖藏起来待来日按陈酒价格出售，t年末总收入为
，假定银行的年利率为r，并以连续复利计息，试求窖藏多少年售出可使总收入的现值最大．并求r＝0.06时的t值．
（14）（本题满分6分）
设函数f（x）在[a，b]上连续，在（a，b）内可导，且f′（x）≠0．试证存在ξ，η∈（a，b），使得
．
（15）（本题满分6分）
设有两条抛物线
，记它们交点的横坐标的绝对值为an．
（Ⅰ）求这两条抛物线所围成的平面图形的面积Sn；
（Ⅱ）求级数
的和．
（16）（本题满分7分）
设函数f（x）在[1，＋∞）上连续．若由曲线y＝f（x），直线x＝1，x＝t（t＞1）与x轴所围成的平面图形绕x轴旋转一周所成的旋转体体积为
试求y＝f（x）所满足的微分方程，并求该微分方程满足条件
的解．
（17）（本题满分9分）
设向量α＝（a1，a2，…，an）T，β＝（b1，b2，…，bn）T都是非零向量，且满足条件αTβ＝0．记n阶矩阵A＝αβT．求：
(Ⅰ)A2;
（Ⅱ）矩阵A的特征值和特征向量.
（18）（本题满分7分）
设矩阵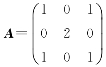
，矩阵B＝（kE＋A）2，其中k为实数，E为单位矩阵.求对角矩阵Λ，使B与Λ相似，并求k为何值时，B为正定矩阵．
（19）（本题满分10分）
一商店经销某种商品，每周进货的数量X与顾客对该种商品的需求量Y是相互独立的随机变量，且都服从区间[10，20]上的均匀分布．商店每售出一单位商品可得利润1000元；若需求量超过了进货量，商店可从其他商店调剂供应，这时每单位商品获利润为500元．试计算此商店经销该种商品每周所得利润的期望值．
（20）（本题满分9分）
设有来自三个地区的各10名，15名和25名考生的报名表，其中女生的报名表分别为3份，7份和5份．随机地取一个地区的报名表，从中先后抽出两份．
（Ⅰ）求先抽到的一份是女生表的概率p；
（Ⅱ）已知后抽到的一份是男生表，求先抽到的一份是女生表的概率q．