2000年全国硕士研究生入学统一考试数学三试题
姓名_______分数_______
一、填空题：1～5小题，每小题3分，共15分．
（4）设随机变量X的概率密度为
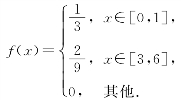
若k使得
，则k的取值范围是_________．
（5）设随机变量X在区间[－1，2]上服从均匀分布，随机变量
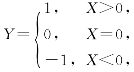
则方差DY＝___________．
二、选择题：6～10小题，每小题3分，共15分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（A）存在且等于零．（B）存在但不一定为零．
（C）一定不存在．（D）不一定存在．
（7）设函数f（x）在点x＝a处可导，则函数|f（x）|在点x＝a处不可导的充分条件是
（A）f（a）＝0且f′（a）＝0．（B）f（a）＝0且f′（a）≠0．
（C）f（a）＞0且f′（a）＞0．（D）f（a）＜0且f′（a）＜0．
（8）设α1，α2，α3是四元非齐次线性方程组AX＝b的三个解向量，且r（A）＝3，α1＝（1，2，3，4）T，α2＋α3＝（0，1，2，3）T，C表示任意常数，则线性方程组AX＝b的通解X＝
（9）设A为n阶实矩阵，AT为A的转置矩阵，则对于线性方程组（Ⅰ）：AX＝0和（Ⅱ）：ATAX＝0，必有
（A）（Ⅱ）的解是（Ⅰ）的解，（Ⅰ）的解也是（Ⅱ）的解．
（B）（Ⅱ）的解是（Ⅰ）的解，但（Ⅰ）的解不是（Ⅱ）的解．
（C）（Ⅰ）的解不是（Ⅱ）的解，（Ⅱ）的解也不是（Ⅰ）的解．
（D）（Ⅰ）的解是（Ⅱ）的解，但（Ⅱ）的解不是（Ⅰ）的解．
（10）在电炉上安装了4个温控器，其显示温度的误差是随机的．在使用过程中，只要有两个温控器显示的温度不低于临界温度t0，电炉就断电．以E表示事件“电炉断电”，而T（1）≤T（2）≤T（3）≤T（4）为4个温控器显示的按递增顺序排列的温度值，则事件E等于
(A){T(1)≥t0}．(B){T(2)≥t0}．
(C){T(3)≥t0}．(D){T(4)≥t0}．
三、解答题：11～19小题，共70分．解答应写出文字说明、证明过程或演算步骤．
（11）（本题满分7分）
求微分方程y″－2y′－e2x＝0满足条件y（0）＝1，y′（0）＝1的解．
（12）（本题满分7分）
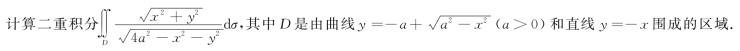
（13）（本题满分7分）
假设某企业在两个相互分割的市场上出售同一种产品，两个市场的需求函数分别是
其中p1和p2分别表示该产品在两个市场的价格（单位：万元/吨），Q1和Q2分别表示该产品在两个市场的销售量（即需求量，单位：吨），并且该企业生产这种产品的总成本函数是
其中Q表示该产品在两个市场的销售总量，即Q＝Q1＋Q2．
（Ⅰ）如果该企业实行价格差别策略，试确定两个市场上该产品的销售量和价格，使该企业获得最大利润；
（Ⅱ）如果该企业实行价格无差别策略，试确定两个市场上该产品的销售量及其统一的价格，使该企业的总利润最大化；并比较两种价格策略下的总利润大小．
（14）（本题满分8分）
求函数
的单调区间和极值，并求该函数图形的渐近线．
（15）（本题满分7分）
（16）（本题满分7分）
设函数f（x）在[0，π]上连续，且
．
试证明：在（0，π）内至少存在两个不同的点ξ1，ξ2，使f（ξ1）＝f（ξ2）＝0．
（17）（本题满分8分）
设向量组α1＝（a，2，10）T，α2＝（－2，1，5）T，α3＝（－1，1，4）T，β＝（1，b，c）T．试问：当a，b，c满足什么条件时，
（Ⅰ）β可由α1，α2，α3线性表示，且表示唯一？
（Ⅱ）β不能由α1，α2，α3线性表示？
（Ⅲ）β可由α1，α2，α3线性表示，但表示不唯一？并求出一般表达式．
（18）（本题满分10分）
设有n元实二次型
其中ai（i＝1，2，…，n）为实数．试问：当a1，a2，…，an满足何种条件时，二次型f（x1，x2，…，xn）为正定二次型．
（19）（本题满分9分）
设A，B是两个随机事件，随机变量
试证明随机变量X和Y不相关的充分必要条件是A与B相互独立．