2008年全国硕士研究生入学统一考试数学三试题
姓名_______分数_______
一、选择题：1～8小题，每小题4分，共32分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（1）设函数f（x）在区间[－1，1]上连续，则x＝0是函数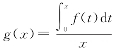
的
（A）跳跃间断点．（B）可去间断点．
（C）无穷间断点．（D）振荡间断点．
（2）如图所示，曲线段的方程为y＝f（x），函数f（x）在区间[0，a]上有连续的导数，则定积分
等于
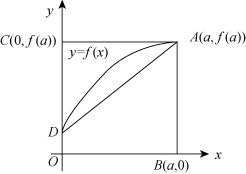
（A）曲边梯形ABOD的面积．
（B）梯形ABOD的面积．
（C）曲边三角形ACD的面积．
（D）三角形ACD的面积．
（3）已知
，则
（A）f′x（0，0），f′y（0，0）都存在．
（B）f′x（0，0）不存在，f′y（0，0）存在．
（C）f′x（0，0）存在，f′y（0，0）不存在．
（D）f′x（0，0），f′y（0，0）都不存在．
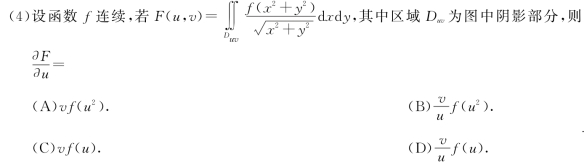
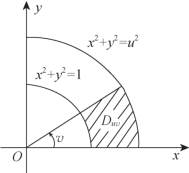
（5）设A为n阶非零矩阵，E为n阶单位矩阵，若A3＝O，则
（A）E－A不可逆，E＋A不可逆．
（B）E－A不可逆，E＋A可逆．
（C）E－A可逆，E＋A可逆．
（D）E－A可逆，E＋A不可逆．
（6）设
则，在实数域上与A合同的矩阵为
（7）设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z＝max{X，Y}的分布函数为
(A)F2(x).(B)F(x)F(y).
(C)1－[1－F(x)]2.(D)[1－F(x)][1－F(y)].
（8）设随机变量X～N（0，1），Y～N（1，4），且相关系数ρXY＝1，则
(A)P{Y＝－2X－1}＝1.(B)P{Y＝2X－1}＝1.
(C)P{Y＝－2X＋1}＝1.(D)P{Y＝2X＋1}＝1.
二、填空题：9～14小题，每小题4分，共24分．
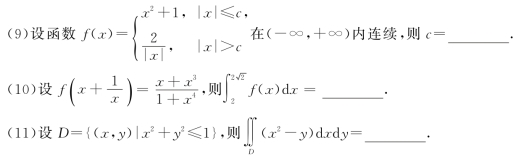
（12）微分方程xy′＋y＝0满足条件y（1）＝1的解是y＝_________.
（13）设3阶矩阵A的特征值为1，2，2，E为3阶单位矩阵，则|4A－1－E|＝_________.
（14）设随机变量X服从参数为1的泊松分布，则P{X＝E（X2）}＝_________.
三、解答题：15～23小题，共94分．解答应写出文字说明、证明过程或演算步骤．
（15）（本题满分9分）
（16）（本题满分10分）
设z＝z（x，y）是由方程x2＋y2－z＝φ（x＋y＋z）所确定的函数，其中φ具有二阶导数，且φ′≠－1.
（Ⅰ）求dz；
（Ⅱ）记
（17）（本题满分11分）
计算
，其中D＝{（x，y）|0≤x≤2，0≤y≤2}.
（18）（本题满分10分）
设f（x）是周期为2的连续函数．
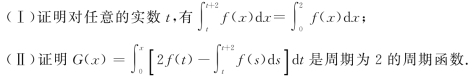
（19）（本题满分10分）
设银行存款的年利率为r＝0．05，并依年复利计算．某基金会希望通过存款A万元实现第一年提取19万元，第二年提取28万元，…，第n年提取（10＋9n）万元，并能按此规律一直提取下去，问A至少应为多少万元？
（20）（本题满分12分）
设n元线性方程组Ax＝b，其中
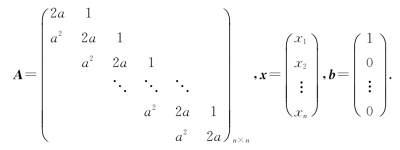
（Ⅰ）证明行列式|A|＝（n＋1）an；
（Ⅱ）当a为何值时，该方程组有唯一解，并求x1；
（Ⅲ）当a为何值时，该方程组有无穷多解，并求通解．
（21）（本题满分10分）
设A为3阶矩阵，α1，α2为A的分别属于特征值－1，1的特征向量，向量α3满足Aα3＝α2＋α3.
（Ⅰ）证明α1，α2，α3线性无关；
（Ⅱ）令P＝（α1，α2，α3），求P－1AP.
（22）（本题满分11分）
设随机变量X与Y相互独立，X的概率分布为
，Y的概率密度为
（Ⅰ）求
；
（Ⅱ）求Z的概率密度fZ（z）.
（23）（本题满分11分）
设X1，X2，…，Xn是总体N（μ，σ2）的简单随机样本．记
（Ⅰ）证明T是μ2的无偏估计量；（证明ET＝μ2即可）
（Ⅱ）当μ＝0，σ＝1时，求DT.