（试卷Ⅳ）
一、填空题（本题共5小题，每小题3分，满分15分）
二、选择题（本题共5小题，每小题3分，满分15分）
（1）设f（x）＝2x＋3x－2，则当x→0时
（A）f（x）是x的等价无穷小．（B）f（x）与x是同阶但非等价无穷小．
（C）f（x）是比x更高阶的无穷小．（D）f（x）是比x较低阶的无穷小．
（2）在下列等式中，正确的结果是
（3）设A为n阶方阵且|A|＝0，则
（A）A中必有两行（列）的元素对应成比例．
（B）A中任意一行（列）向量是其余各行（列）向量的线性组合．
（C）A中必有一行（列）向量是其余各行（列）向量的线性组合．
（D）A中至少有一行（列）的元素全为0.
（4）设A和B都是n×n矩阵，则必有
(A)|A＋B|＝|A|＋|B|．(B)AB＝BA．(C)|AB|＝|BA|．(D)(A＋B)－1＝A－1＋B－1．
（5）以A表示事件“甲种产品畅销，乙种产品滞销”，则其对立事件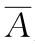
为
（A）“甲种产品滞销，乙种产品畅销”.（B）“甲、乙两种产品均畅销”.
（C）“甲种产品滞销”.（D）“甲种产品滞销或乙种产品畅销”.
三、（本题共3小题，每小题5分，满分15分）
（1）求极限
．
（2）已知z＝f（u，v），u＝x＋y，v＝xy，且f（u，v）的二阶偏导数都连续，求
．
（3）求微分方程y″＋5y′＋6y＝2e－x的通解．
四、（本题满分9分）
设某厂家打算生产一批商品投放市场，已知该商品的需求函数为
，且最大需求量为6，其中x表示需求量，p表示价格．
（1）求该商品的收益函数和边际收益函数；（2）求使收益最大时的产量，最大收益和相应的价格；（3）画出收益函数的图形．
五、（本题满分9分）
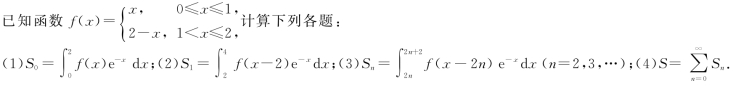
六、（本题满分6分）
假设函数f（x）在[a，b]上连续，在（a，b）内可导，且
证明在（a，b）内F′（x）≤0.
七、（本题满分5分）已知X＝AX＋B，其中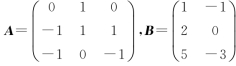
，求矩阵X．
八、（本题满分6分）
设α1＝（1，1，1），α2＝（1，2，3），α3＝（1，3，t）．问：
（1）当t为何值时，向量组α1，α2，α3线性无关？（2）当t为何值时，向量组α1，α2，α3线性相关？
（3）当向量组α1，α2，α3线性相关时，将α3表示为α1和α2的线性组合．
九、（本题满分5分）
设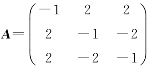
．
（1）试求矩阵A的特征值；（2）利用（1）的结果，求矩阵E＋A－1的特征值，其中E是3阶单位矩阵．
十、（本题满分7分）
已知随机变量X和Y的联合概率密度为
试求：（1）P{X＜Y}；（2）E（XY）．
十一、（本题满分8分）
设随机变量X在[2，5]上服从均匀分布，现在对X进行三次独立观测，试求至少有两次观测值大于3的概率．