（试卷Ⅳ）
一、填空题（本题共5小题，每小题3分，满分15分）
（2）设f（x）有连续的导数，f（0）＝0且f′（0）＝b，若函数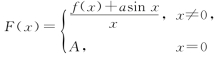
在x＝0处连续，则常数A＝_________.
（3）曲线y＝x 2与直线y＝x＋2所围成的平面图形面积为_______.
（4）若线性方程组
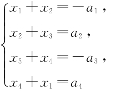
有解，则常数a 1，a 2，a 3，a 4应满足条件_______.
（5）一射手对同一目标独立地进行4次射击，若至少命中一次的概率为
，则该射手的命中率为_______.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）设函数f（x）＝x tan x esin x，则f（x）是
（A）偶函数．（B）无界函数．（C）周期函数．（D）单调函数．
（2）设函数f（x）对任意的x均满足等式f（1＋x）＝af（x），且有f′（0）＝b，其中a，b为非零常数，则
（A）f（x）在x＝1处不可导．（B）f（x）在x＝1处可导，且f′（1）＝a.
（C）f（x）在x＝1处可导，且f′（1）＝b.（D）f（x）在x＝1处可导，且f′（1）＝ab.
（3）向量组α1，α2，…，αs线性无关的充分条件是
（A）α1，α2，…，αs均不为零向量．
（B）α1，α2，…，αs中任意两个向量的分量不成比例．
（C）α1，α2，…，αs中任意一个向量均不能由其余s－1个向量线性表示．
（D）α1，α2，…，αs中有一部分向量线性无关．
（4）设A，B为两个随机事件，且B⊂A，则下列式子中正确的是
(A)P(A＋B)＝P(A).(B)P(AB)＝P(A).
(C)P(B|A)＝P(B).(D)P(B－A)＝P(B)－P(A).
（5）设随机变量X和Y相互独立，其概率分布为
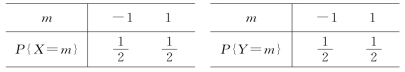
则下列式子正确的是
三、（本题共4小题，每小题5分，满分20分）
（4）求微分方程y′＋y cos x＝（ln x）e－sin x的通解．
四、（本题满分9分）
某公司可通过电台及报纸两种方式做销售某种商品的广告，根据统计资料，销售收入R（万元）与电台广告费用x 1（万元）及报纸广告费用x 2（万元）之间的关系有如下经验公式
（1）在广告费用不限的情况下，求最优广告策略；（2）若提供的广告费用为1.5万元，求相应的最优广告策略．
五、（本题满分6分）
设f（x）在闭区间[0，c]上连续，其导数f′（x）在开区间（0，c）内存在且单调减少，f（0）＝0，试应用拉格朗日中值定理证明不等式f（a＋b）≤f（a）＋f（b），其中常数a，b满足条件0≤a≤b≤a＋b≤c．
六、（本题满分8分）
（1）a，b为何值时，方程组有解？（2）方程组有解时，求出方程组的导出组的一个基础解系；
（3）方程组有解时，求出方程组的全部解．
七、（本题满分5分）
已知对于n阶方阵A，存在自然数k，使A k＝O．试证明矩阵E－A可逆，并写出其逆矩阵的表达式（E为n阶单位阵）．
八、（本题满分6分）
设A为n阶矩阵，λ1和λ2是A的两个不同的特征值，x 1，x 2是分别属于λ1和λ2的特征向量．试证明x 1＋x 2不是A的特征向量．
九、（本题满分4分）
从0，1，2，…，9等十个数字中任意选出三个不同的数字，试求下列事件的概率：A 1＝{三个数字中不含0和5}；A 2＝{三个数字中不含0或5}；A 3＝{三个数字中含0但不含5}．
十、（本题满分5分）
一电子仪器由两个部件构成，以X和Y分别表示两个部件的寿命（单位：千小时），已知X和Y的联合分布函数为
（1）问X和Y是否独立？（2）求两个部件的寿命都超过100小时的概率α.
十一、（本题满分7分）
某地抽样调查结果表明，考生的外语成绩（百分制）近似服从正态分布，平均成绩为72分，96分以上的占考生总数的2.3%，试求考生的外语成绩在60分至84分之间的概率．
[附表]（表中Φ（x）是标准正态分布函数）
