（试卷Ⅴ）
一、填空题（本题共5小题，每小题3分，满分15分）
（2）【同试卷Ⅳ 第一、（2）题】
（3）【同试卷Ⅳ 第一、（3）题】
（4）【同试卷Ⅳ 第一、（4）题】
（5）设X是一个随机变量，其概率密度为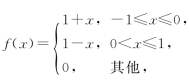
则方差DX＝_________.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）【同试卷Ⅳ 第二、（1）题】
（2）【同试卷Ⅳ 第二、（2）题】
（3）设n维行向量
，矩阵A＝E－αTα，B＝E＋2αTα，其中E为n阶单位矩阵，则AB等于
(A)O.(B)－E.(C)E.(D)E＋αTα.
（4）设矩阵Am×n的秩为r（A）＝m＜n，Em为m阶单位矩阵，下述结论中正确的是
（A）A的任意m个列向量必线性无关．
（B）A的任意一个m阶子式不等于零．
（C）非齐次线性方程组Ax＝b一定有无穷多解．
（D）A通过初等行变换，必可以化为（Em O）的形式．
（5）【同试卷Ⅳ 第二、（5）题】
三、（本题满分6分）【同试卷Ⅳ 第三题】
四、（本题满分6分）
求不定积分
．
五、（本题满分7分）【同试卷Ⅳ 第八题】
六、（本题满分6分）【同试卷Ⅳ 第七题】
七、（本题满分5分）
设f（x）在区间[a，b]上连续，在（a，b）内可导，证明：在（a，b）内至少存在一点ξ，使
．
八、（本题满分9分）
求二元函数z＝f（x，y）＝x2y（4－x－y）在由直线x＋y＝6，x轴和y轴所围成的闭区域D上的极值、最大值与最小值．
九、（本题满分8分）
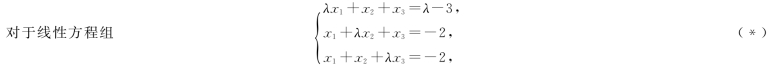
讨论λ取何值时，方程组有唯一解、无解和无穷多解．在方程组有无穷多解时，试用其导出组的基础解系表示全部解．
十、（本题满分8分）
设3阶矩阵A满足Aαi＝iαi（i＝1，2，3），其中列向量α1＝（1，2，2）T，α2＝（2，－2，1）T，α3＝（－2，－1，2）T．试求矩阵A．
十一、（本题满分8分）【同试卷Ⅳ 第十一题】
十二、（本题满分7分）
假设随机变量X服从参数为2的指数分布，证明：Y＝1－e－2X在区间（0，1）上服从均匀分布．