1997年全国硕士研究生入学统一考试数学三试题
姓名_______分数_______
一、填空题：1～5小题，每小题3分，共15分．
（1）设y＝f（lnx）ef（x），其中f可微，则dy＝___________．
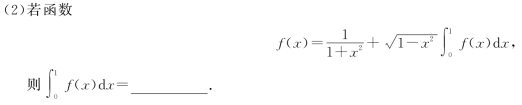
（3）差分方程yt＋1－yt＝t2t的通解为_________．
（5）设随机变量X和Y相互独立且都服从正态分布N（0，32），而X1，…，X9和Y1，…，Y9分别是来自总体X和Y的简单随机样本，则统计量
服从_________分布，参数为_________．
二、选择题：6～10小题，每小题3分，共15分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（6）设函数
则当x→0时，f（x）是g（x）的
（A）低阶无穷小．（B）高阶无穷小．
（C）等价无穷小．（D）同阶但不等价的无穷小．
（7）若函数f（－x）＝f（x）（－∞＜x＜＋∞），在（－∞，0）内f′（x）＞0且f″（x）＜0，则在（0，＋∞）内有
(A)f′(x)＞0,f″(x)＜0．(B)f′(x)＞0,f″(x)＞0．
(C)f′(x)＜0,f″(x)＜0．(D)f′(x)＜0,f″(x)＞0．
（8）设向量组α1，α2，α3线性无关，则下列向量组中，线性无关的是
(A)α1＋α2,α2＋α3,α3－α1．
(B)α1＋α2,α2＋α3,α1＋2α2＋α3．
(C)α1＋2α2,2α2＋3α3,3α3＋α1．
(D)α1＋α2＋α3,2α1－3α2＋22α3,3α1＋5α2－5α3．
（9）设A，B为同阶可逆矩阵，则
（A）AB＝BA．（B）存在可逆矩阵P，使P－1AP＝B．
（C）存在可逆矩阵C，使CTAC＝B．（D）存在可逆矩阵P和Q，使PAQ＝B．
（10）设两个随机变量X与Y相互独立且同分布：
，而下列各式中成立的是
三、解答题：11～21小题，共70分．解答应写出文字说明、证明过程或演算步骤．
（11）（本题满分6分）
在经济学中，称函数
为固定替代弹性生产函数，而称函数Q＝AKδL1－δ为Cobb－Douglas生产函数（简称C－D生产函数）．
试证明：当x→0时，固定替代弹性生产函数变为C－D生产函数，即有
．
（12）（本题满分5分）
设u＝f（x，y，z）有连续偏导数，y＝y（x）和z＝z（x）分别由方程exy－y＝0和ez－xz＝0所确定，求
．
（13）（本题满分6分）
一商家销售某种商品的价格满足关系p＝7－0.2x（万元/吨），x为销售量（单位：吨），商品的成本函数是C＝3x＋1（万元）．
（Ⅰ）若每销售一吨商品，政府要征税t（万元），求该商家获最大利润时的销售量；
（Ⅱ）t为何值时，政府税收总额最大．
（14）（本题满分6分）
设函数f（x）在[0，＋∞）上连续、单调不减且f（0）≥0．试证函数
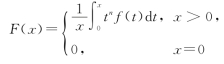
在[0，＋∞）上连续且单调不减（其中n＞0）．
（15）（本题满分6分）
从点P1（1，0）作x轴的垂
线，交抛物线y＝x2于点Q1（1，1）；再从Q1作这条抛物线的切线与x轴交于P2．然后又从P2作x轴的垂线，交抛物线于点Q2，依次重复上述过程得到一系列的点P1，Q1；P2，Q2；…；Pn，Qn；…．
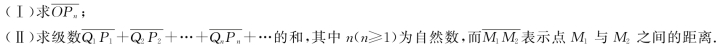
（16）（本题满分6分）
设函数f（t）在[0，＋∞）上连续，且满足方程
，求f（t）．
（17）（本题满分6分）
设A为n阶非奇异矩阵，α为n维列向量，b为常数．记分块矩阵
其中A*是矩阵A的伴随矩阵，E为n阶单位矩阵．
（Ⅰ）计算并化简PQ；
（Ⅱ）证明：矩阵Q可逆的充分必要条件是αTA－1α≠b．
（18）（本题满分10分）
设3阶实对称矩阵A的特征值是1，2，3；矩阵A的属于特征值1，2的特征向量分别是α1＝（－1，－1，1）T，α2＝（1，－2，－1）T．
（Ⅰ）求A的属于特征值3的特征向量；
（Ⅱ）求矩阵A．
（19）（本题满分7分）
假设随机变量X的绝对值不大于1，
，在事件{－1＜X＜1}出现的条件下，X在（－1，1）内的任一子区间上取值的条件概率与该子区间长度成正比．试求X的分布函数．
（20）（本题满分6分）
游客乘电梯从底层到电视塔顶层观光，电梯于每个整点的第5分钟，25分钟和55分钟从底层起行．假设一游客在早八点的第X分钟到达底层候梯处，且X在[0，60]上均匀分布，求该游客等候时间的数学期望．
（21）（本题满分6分）
两台同样的自动记录仪，每台无故障工作的时间服从参数为5的指数分布．首先开动其中一台，当其发生故障时停用而另一台自行开动．试求两台记录仪无故障工作的总时间T的概率密度f（t），数学期望和方差．