2015年全国硕士研究生招生考试数学三试题
姓名_______分数_______
一、选择题：1～8小题，每小题4分，共32分．下列每题给出的四个选项中，只有一个选项是符合题目要求的．
（1）设{xn}是数列．下列命题中不正确的是
（2）设函数f（x）在（－∞，＋∞）内连续，其二阶导函数f″（x）的图形如右图所示，则曲线y＝f（x）的拐点个数为
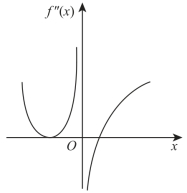
(A)0.(B)1.
(C)2.(D)3.
（3）设D＝{（x，y）|x2＋y2≤2x，x2＋y2≤2y}，函数f（x，y）在D上连续，则
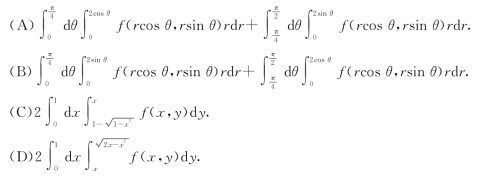
（4）下列级数中发散的是
（5）设矩阵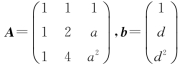
.若集合Ω＝{1，2}，则线性方程组Ax＝b有无穷多解的充分必要条件为
(A)a∉Ω,d∉Ω.(B)a∉Ω,d∈Ω.
(C)a∈Ω,d∉Ω.(D)a∈Ω,d∈Ω.
（6）设二次型f（x1，x2，x3）在正交变换x＝Py下的标准形为
，其中P＝（e1，e2，e3）.若Q＝（e1，－e3，e2），则f（x1，x2，x3）在正交变换x＝Qy下的标准形为
（7）若A，B为任意两个随机事件，则
（8）设总体X～B（m，θ），X1，X2，…，Xn为来自该总体的简单随机样本，¯X为样本均值，则
(A)(m－1)nθ(1－θ).(B)m(n－1)θ(1－θ).
(C)(m－1)(n－1)θ(1－θ).(D)mnθ(1－θ).
二、填空题：9～14小题，每小题4分，共24分．
（12）设函数y＝y（x）是微分方程y″＋y′－2y＝0的解，且在x＝0处y（x）取得极值3，则y（x）＝_________.
（13）设3阶矩阵A的特征值为2，－2，1，B＝A2－A＋E，其中E为3阶单位矩阵，则行列式|B|＝_________..
（14）设二维随机变量（X，Y）服从正态分布N（1，0；1，1；0），则P{XY－Y＜0}＝_________.
三、解答题：15～23小题，共94分．解答应写出文字说明、证明过程或演算步骤．
（15）（本题满分10分）
设函数f（x）＝x＋aln（1＋x）＋bxsinx，g（x）＝kx3.若f（x）与g（x）在x→0时是等价无穷小，求a，b，k的值．
（16）（本题满分10分）
计算二重积分
，其中D＝{（x，y）|x2＋y2≤2，y≥x2}.
（17）（本题满分10分）
为了实现利润最大化，厂商需要对某商品确定其定价模型．设Q为该商品的需求量，p为价格，MC为边际成本，η为需求弹性（η＞0）.
（Ⅰ）证明定价模型为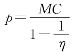
；
（Ⅱ）若该商品的成本函数为C（Q）＝1600＋Q2，需求函数为Q＝40－p，试由（Ⅰ）中的定价模型确定此商品的价格．
（18）（本题满分10分）
设函数f（x）在定义域I上的导数大于零．若对任意的x0∈I，曲线y＝f（x）在点（x0，f（x0））处的切线与直线x＝x0及x轴所围成区域的面积恒为4，且f（0）＝2，求f（x）的表达式．
（19）（本题满分10分）
（Ⅰ）设函数u（x），v（x）可导，利用导数定义证明[u（x）v（x）]′＝u′（x）v（x）＋u（x）v′（x）；
（Ⅱ）设函数u1（x），u2（x），…，un（x）可导，f（x）＝u1（x）u2（x）…un（x），写出f（x）的求导公式．
（20）（本题满分11分）
设矩阵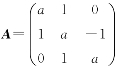
，且A3＝O.
（Ⅰ）求a的值；
（Ⅱ）若矩阵X满足X－XA2－AX＋AXA2＝E，其中E为3阶单位矩阵，求X.
（21）（本题满分11分）
（Ⅰ）求a，b的值；
（Ⅱ）求可逆矩阵P，使P－1AP为对角矩阵．
（22）（本题满分11分）
设随机变量X的概率密度为
对X进行独立重复的观测，直到第2个大于3的观测值出现时停止，记Y为观测次数．
（Ⅰ）求Y的概率分布；
（Ⅱ）求EY.
（23）（本题满分11分）
设总体X的概率密度为
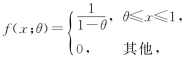
其中θ为未知参数．X1，X2，…，Xn为来自该总体的简单随机样本．
（Ⅰ）求θ的矩估计量；
（Ⅱ）求θ的最大似然估计量．