（试卷Ⅳ）
一、填空题（本题共5小题，每小题3分，满分15分）
（1）设商品的需求函数Q＝100－5p，其中Q，p分别表示需求量和价格，如果商品需求弹性的绝对值大于1，则商品价格的取值范围是_______.
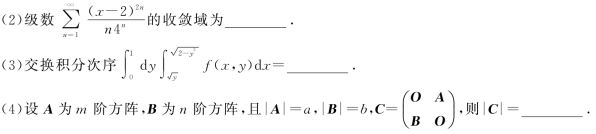
（5）将C，C，E，E，I，N，S这七个字母随机地排成一行，则恰好排成SCIENCE的概率为_______.
二、选择题（本题共4小题，每小题3分，满分12分）
（A）a 2.（B）a 2 f（a）.（C）0.（D）不存在．
（2）当x→0时，下列四个无穷小量中，哪一个是比其他三个更高阶的无穷小量？
(A)x 2.(B)1－cos x.(C)
(D)x－tan x.
（3）设A为m×n矩阵，则齐次线性方程组AX＝0仅有零解的充分条件是
（A）A的列向量线性无关．（B）A的列向量线性相关．
（C）A的行向量线性无关．（D）A的行向量线性相关．
（4）设当事件A与B同时发生时，事件C必发生，则
(A)P(C)≤P(A)＋P(B)－1.(B)P(C)≥P(A)＋P(B)－1.
(C)P(C)＝P(AB).(D)P(C)＝P(A∪B).
三、（本题满分5分）
设函数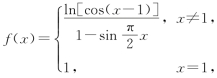
问函数f（x）在x＝1处是否连续？若不连续，修改函数在x＝1处的定义，使之连续．
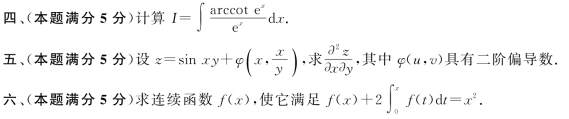
七、（本题满分6分）求证：当x≥1时
．
八、（本题满分9分）
设曲线方程为y＝e－x（x≥0）．
（1）把曲线y＝e－x，x轴，y轴和直线x＝ξ（ξ＞0）所围平面图形绕x轴旋转一周，得一旋转体，求此旋转体体积V（ξ）；求满足
的a．
（2）在此曲线上找一点，使过该点的切线与两个坐标轴所夹平面图形的面积最大，并求出该面积．
九、（本题满分7分）
设矩阵A与B相似，其中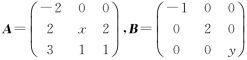
．
（1）求x和y的值；（2）求可逆矩阵P，使P－1 AP＝B．
十、（本题满分6分）
已知3阶矩阵B≠O，且B的每一个列向量都是以下方程组的解：
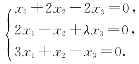
（1）求λ的值；（2）证明|B|＝0．
十一、（本题满分6分）设A，B分别为m阶，n阶正定矩阵，试判定分块矩阵
是否是正定矩阵．
十二、（本题满分8分）
假设测量的随机误差X～N（0，102），试求在100次独立重复测量中，至少有三次测量误差的绝对值大于19.6的概率α，并利用泊松分布求出α的近似值（要求小数点后取两位有效数字）.
注：Φ（1．96）＝0．975，另附表
十三、（本题满分6分）
一台设备由三大部件构成，在设备运转中各部件需要调整的概率相应为0.10，0.20和0.30.假设各部件的状态相互独立，以X表示同时需要调整的部件数，试求X的概率分布，数学期望EX和方差DX.
十四、（本题满分5分）
设二维随机变量（X，Y）的概率密度为
（1）求X的概率密度f X（x）；（2）求概率P{X＋Y≤1}.