（试卷Ⅳ）
一、填空题（本题共4小题，每空1分，满分10分）
（1）设
，则
①f′（x）＝_________； ②f（x）的单调性是_______；
③f（x）的奇偶性是_______；④其图形的拐点是_______；
⑤凹凸区间是_______；⑥水平渐近线是_______.
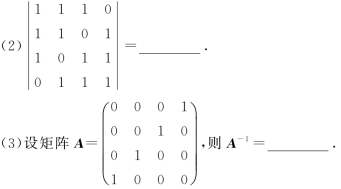
（4）设P（A）＝0.4，P（A∪B）＝0.7，那么
①若A与B互不相容，则P（B）＝_________.
②若A与B相互独立，则P（B）＝_________.
二、判断题（本题共5小题，每小题2分，满分10分）
（4）若A和B都是n阶非零方阵，且AB＝O，则A的秩必小于n.（ ）
（5）若事件A，B，C满足等式A∪C＝B∪C，则A＝B.（ ）
三、（本题共4小题，每小题4分，满分16分）
四、（本题共2小题，每小题3分，满分6分）
五、（本题满分8分）
已知某商品的需求量D和供给量S都是价格p的函数：
其中a＞0和b＞0为常数；价格p是时间t的函数且满足方程
假设当t＝0时价格为1，试求：
（1）需求量等于供给量时的均衡价格p e；
（2）价格函数p（t）；
（3）极限
．
六、（本题满分8分）
在曲线y＝x 2（x≥0）上某点A处作一切线，使之与曲线以及x轴所围图形（如右图）的面积为
，试求：
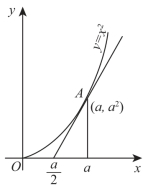
（1）切点A的坐标；
（2）过切点A的切线方程；
（3）由上述所围平面图形绕x轴旋转一周所成旋转体的体积．
七、（本题满分8分）
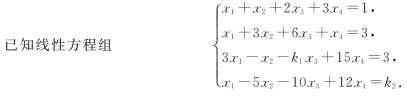
问k 1和k 2各取何值时，方程组无解？有唯一解？有无穷多解？在方程组有无穷多解的情形下，试求出一般解．
八、（本题满分8分）
已知向量组α1，α2，…，αs（s≥2）线性无关．设β1＝α1＋α2，β2＝α2＋α3，…，βs－1＝αs－1＋αs，βs＝αs＋α1．试讨论向量组β1，β2，…，βs的线性相关性．
九、（本题满分7分）
设A是3阶方阵，A*是A的伴随矩阵，A的行列式
，求行列式|（3A）－1－2A*|的值．
十、（本题满分7分）
玻璃杯成箱出售，每箱20只．假设各箱含0，1，2只残次品的概率相应为0.8，0.1和0.1.一顾客欲购一箱玻璃杯，在购买时，售货员随意取一箱，而顾客随机地察看4只：若无残次品，则买下该箱玻璃杯，否则退回．试求：
（1）顾客买下该箱的概率α；
（2）在顾客买下的一箱中，确实没有残次品的概率β.
十一、（本题满分6分）
某保险公司多年统计资料表明，在索赔户中被盗索赔户占20%，以X表示在随意抽查的100个索赔户中因被盗向保险公司索赔的户数．
（1）写出X的概率分布；
（2）利用棣莫弗－拉普拉斯定理，求出被盗索赔户不少于14户且不多于30户的概率的近似值．
（Φ（2．5）＝0．9938，Φ（1．5）＝0．9332，其中Φ（x）为标准正态分布函数）
十二、（本题满分6分）
假设随机变量X在区间（1，2）上服从均匀分布．试求随机变量Y＝e2X的概率密度f（y）.