（试卷Ⅳ）
一、填空题（本题共5小题，每小题3分，满分15分）
二、选择题（本题共5小题，每小题3分，满分15分）
（A）发散．（B）条件收敛．（C）绝对收敛．（D）敛散性与λ有关．
（3）设A是m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r，矩阵B＝AC的秩为r 1，则
(A)r＞r 1.(B)r＜r 1.
（C）r＝r 1.（D）r与r 1的关系依C而定．
（4）设
，则事件A和B
（A）互不相容．（B）互相对立．（C）不独立．（D）独立．
（5）设X 1，X 2，…，X n是来自正态总体N（μ，σ2）的简单随机样本，¯X是样本均值，记
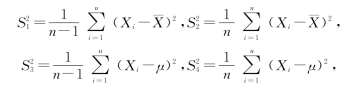
则服从自由度为n－1的t分布的随机变量是
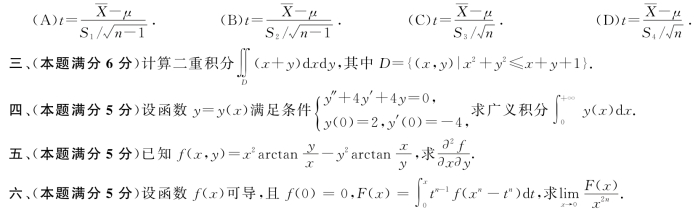
七、（本题满分8分）
已知曲线
与曲线
在点（x 0，y 0）处有公共切线．求
（1）常数a及切点（x 0，y 0）；（2）两曲线与x轴围成的平面图形绕x轴旋转所得旋转体的体积V x．
八、（本题满分6分）
假设f（x）在[a，＋∞）上连续，f″（x）在（a，＋∞）内存在且大于零，记
）．证明：F（x）在（a，＋∞）内单调增加．
九、（本题满分11分）
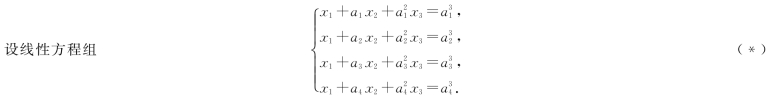
（1）证明：若a 1，a 2，a 3，a 4两两不相等，则此线性方程组无解；
（2）设a 1＝a 3＝k，a 2＝a 4＝－k（k≠0），且已知β1，β2是该方程组的两个解，其中β1＝（－1，1，1）T，β2＝（1，1，－1）T，写出此方程组的通解．
十、（本题满分8分）
设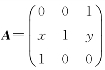
有三个线性无关的特征向量，求x和y应满足的条件．
十一、（本题满分8分）
假设随机变量X 1，X 2，X 3，X 4相互独立，且同分布，P{X i＝0}＝0.6，P{X i＝1}＝0.4（i＝1，2，3，4）.求行列式X＝
的概率分布．
十二、（本题满分8分）
假设由自动线加工的某种零件的内径X（毫米）服从正态分布N（μ，1），内径小于10或大于12为不合格品，其余为合格品．销售每件合格品获利，销售每件不合格品亏损，已知销售利润T（单位：元）与销售零件的内径X有如下关系：
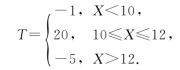
问平均内径μ取何值时，销售一个零件的平均利润最大？