（试卷Ⅳ）
一、填空题（本题共4小题，每小题3分，满分12分）
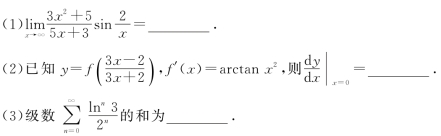
（4）设4阶方阵A的秩为2，则其伴随矩阵A*的秩为_______.
二、选择题（本题共5小题，每小题3分，满分15分）
（1）设函数
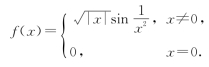
则f（x）在x＝0处
（A）极限不存在．（B）极限存在但不连续．（C）连续但不可导．（D）可导．
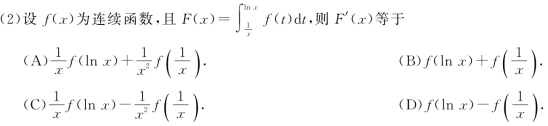
（3）n阶方阵A具有n个不同的特征值是A与对角阵相似的
（A）充分必要条件．（B）充分而非必要条件．
（C）必要而非充分条件．（D）既非充分也非必要条件．
（4）设两事件A与B满足P（B|A）＝1，则
（A）A是必然事件．（B）P（B|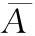
）＝0.（C）A⊃B.（D）A⊂B.
（5）设随机变量X的概率密度为φ（x），且φ（－x）＝φ（x），F（x）为X的分布函数，则对任意实数a，有
三、（本题满分6分）
设z＝f（x，y）是由方程z－y－x＋x e z－y－x＝0所确定的二元函数，求d z．
四、（本题满分7分）
已知
，求常数a的值．
五、（本题满分9分）
设某产品的成本函数为C＝aq 2＋bq＋c，需求函数为
，其中C为成本，q为需求量（即产量），p为单价，a，b，c，d，e都是正的常数，且d＞b，求：
（1）利润最大时的产量及最大利润；（2）需求对价格的弹性；
（3）需求对价格弹性的绝对值为1时的产量．
六、（本题满分8分）
假设：
①函数y＝f（x）（0≤x＜＋∞）满足条件f（0）＝0和0≤f（x）≤e x－1；
②平行于y轴的动直线MN与曲线y＝f（x）和y＝e x－1分别相交于点P 1和P 2；
③曲线y＝f（x）、直线MN与x轴所围封闭图形的面积S恒等于线段P 1 P 2的长度．
求函数y＝f（x）的表达式．
七、（本题满分7分）
假设函数f（x）在[0，1]上连续，在（0，1）内二阶可导，过点A（0，f（0））与B（1，f（1））的直线与曲线y＝f（x）相交于点C（c，f（c）），其中0＜c＜1.证明：在（0，1）内至少存在一点ξ，使f″（ξ）＝0．
八、（本题满分10分）
k为何值时，线性方程组
有唯一解、无解、有无穷多解？在有解情况下，求出其全部解．
九、（本题满分9分）
十、（本题满分9分）
设随机变量X和Y同分布，X的概率密度为
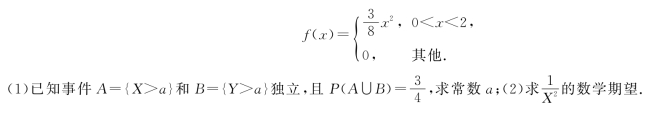
十一、（本题满分8分）
假设一大型设备在任何长为t的时间内发生故障的次数N（t）服从参数为λt的泊松分布．
（1）求相继两次故障之间时间间隔T的概率分布；
（2）求在设备已无故障工作8小时的情形下，再无故障运行8小时的概率Q.