依托生活情境材料,设计生活化的学习问题
由于具体的情境材料和学生的现实生活息息相关,因此,要设计出能激发想象力和探索力的问题。同时,问题应具有开放性,即问题解决方式的途径和方法不唯一。设计出的问题应具有3个重要的特征:第一,来源于学生的现实生活,让学生感觉到这个问题就存在于生活中,与自己有密切的联系;第二,这个问题背后隐含着相关的教学内容和教学目标,通过问题的探究能让学生获得知识;第三,问题的指向性明确,学生要想解决问题就必须对问题进行综合的分析,设计解决问题的方案。由此依托情境材料设计出来的问题,学生在解决时要付出一定的努力,学生在尝试解决问题的过程中有很大的自主探究和创造空间。
(一)依据课程标准,设计开放性的生活化学习问题
《义务教育数学课程标准(2011年版)》的总体目标具体表现在知识与技能、数学思考、问题解决及情感态度4个维度。这4个维度正是我们设计问题需要充分考虑的。从知识技能目标来看,要求学生经历探究的过程后掌握基础知识和基本技能;在实现数学思考目标和问题解决目标上,要求在问题的引领下让学生经历解决问题的过程,发展学生的形象思维和抽象思维能力;学生在探究学习的过程中逐步形成独立思考的习惯和实事求是的态度。因此,依据《义务教育数学课程标准(2011年版)》中的四维目标设计数学问题更具有开发性,不仅要求学生学习问题背后的数学知识,更重要的是让学生体验探究问题的过程并发展解决问题的能力。
例如,在“长、正方体表面积和体积练习”一课中,设计了这样一个教学环节:
同学们帮助茶厂工人将长和宽各为20 cm,高为10 cm的长方体茶盒装入棱长为30cm的正方体纸箱,最多能装几盒?怎样才能装下?
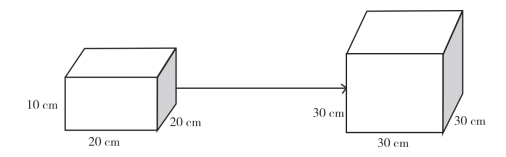
遇到生活中的实际问题,长方体的体积计算就变得更复杂,需要多角度去考虑问题,通过不断的尝试和调整,再进行对比,最终才能找到解决问题的正确方法。
在解决长方体包装盒的问题时,学生的生活经验是有的,但他们的经验往往停留在实际操作层面,很少有人将计算与实际摆放结合思考并优化。数学课堂教学就是要让学生学会用数学的眼光观察世界,并用数学的思维分析问题。
(二)借助多媒体,设计层次性的生活化学习问题
根据皮亚杰的儿童认知发展理论,小学生正好处于“具体运算阶段”,其认知结构属于“直觉思维图式”阶段。现代教学媒体为教学提供了一种方便、高效、直观的教学手段,借助多媒体设备进行教学,能充分调动学生的各类感官活动,提高学生对教学内容的兴趣。充分利用多媒体直观、生动的特点,让学生的感受变得更加真实,尤其是在图形与几何板块教学中,应利用多媒体制作美丽的数学图案,以丰富学生的视觉。
例如,在四年级下册“三角形的内角和”一课中,有这样的一个教学片段:
师:孩子们,今天老师请来了两位朋友和咱们一起学习,看看它们是谁?
PPT出示:
三角形大胖

三角形小胖
音频动画:
A:大家好,我是三角形大胖,我可比三角形小胖大多啦。
B:你胡说,我可比你大。
A:明明就是我大。
B:我大,A我大……
师:孩子们,大胖和小胖吵得这么厉害,它们在比呀?(比谁大)
师:你认为它们这是在比谁大谁小是吧?那你说说,谁大谁小呢?
生:A大B小。
师:怎么知道的?
生:直接看出来的。
师:那除了比面积的大小,你们认为这两个三角形还可以比什么呢?
生:周长。
师:如果是比周长的话,那又是谁大谁小呢?怎么知道的?
师:其实,老师也不知道它们是在比什么,我们听它们自己说吧。
课件PPT音频:
A:小朋友们,你们来评评理,我的个头这么大,我的内角和一定比它的内角和大。
师:孩子们,你们听明白它们是比什么了吗?
生:内角和。
师:今天我们就来研究三角形的内角和。
在“三角形的内角和”一课中,通过多媒体动画从比周长→比面积→比内角和,设计层次性问题,让学生复习了旧知,也引出了新知,可以感知到内角和与周长、面积是不一样的。
又如,在三年级下册“面积”一课中,在探究面积大小的比较方法中设计了这样的教学环节:
师:请你们摸一摸,观察一下数学书的封面和侧面,谁的面积大;黑板面和国旗面呢?你们是怎样快速比较出来的?
生:一眼看出来的。
师:这样的方法在我们的数学中叫“观察法”。
师:(PPT出示)这两个图形你能一眼看出谁的面积大吗?你有什么方法能判断出它们面积的大小吗?
生:重叠起来。
师:对啦,像这样不是特别明显的我们可以用重叠法来进行比较。
师:(PPT出示)这两个图形哪个面积大?刚刚的观察法和重叠法还行吗?(不行)
师:你有什么方法能判断出它们面积的大小吗?
师:我们一起来听个故事,找找灵感吧!(播放绘本《公主殿下来的那天》,在绘本故事中,采用了相同大小的坐垫来度量)
师:是如何比较出哪张床更大的呢?(相同大小的坐垫)
师:可以选择一种图形作单位来测量,这种方法在数学中叫“度量法”。
师:度量时要统一标准,是怎样的标准呢?(形状大小相同)
面积大小的比较方法有观察法、重叠法和度量法。这节课结合多媒体,通过设计层次性的生活化学习问题来讲解在什么情况下用什么方法来比较面积的大小,拓展了学生的空间观念。
(三)以关键问题为核心,设计生活化学习的问题链
从教学目标和教学内容来看,《义务教育数学课程标准(2011年版)》更加关注学生的问题解决能力的发展,关注实际问题的解决。在目标上,单独将“问题解决”作为课程目标提出;在教学内容上,解决问题的教学并非单一的“解决应用题”的教学,而更强调的是问题的生活化,强调学生实践能力、应用意识的培养,对问题的障碍性和探究性提出了更高的要求。
在问题导向学习中,设计问题链是为了更好地实现预先设定的教学目标,将教学的过程分解为系统化、一连串的数学问题,问题之间围绕同一个中心,有先后序列的关系。毛志峰在《问题导向学习》中强调了问题链对学生学习过程的导引,认为问题链中的问题是一个套一个、一步步深入的,每个问题都是具有思维含量的,问题链将所要解决的中心问题与教学目标紧紧地连接起来。
例如,在三年级下册“面积和面积单位”一课中,在讲授颇具抽象意义的面积单位(平方厘米、平方分米和平方米)时,小学三年级的学生抽象思维能力还很有限。因此,面积单位的理解和掌握也就成了这一节的教学难点。要把抽象的面积单位讲得明白透彻,就要从学生生活中的事物入手,告诉学生1 cm2大约就是我们指甲的大小,由此引导学生思考1 dm2大约有多大,可用身边的什么事物来形容呢?接下来再思考1 m2有多大呢,又可以怎么形容呢?通过这样一连串的问题,可引发学生联系实际生活中的事物来帮助学生在头脑中建立具体形象的面积单位,自然就会收到满意的教学效果。
又如,在“长、正方体表面积和体积练习”一课中,教师以复习长正方体的表面积和体积为核心问题,设计了3个层次性问题的教学环节:
任务一:设计6个面都是长方形的长方体。
任务二:切一刀,得到有两个面是正方形的长方体。
任务三:切出最大的正方体。
教师通过布置这3个有层次性的任务,学生不仅在操作活动中复习了长正方体的表面积和体积,还构建了空间模型,拓展了空间想象力和空间观念。
