在生活实践中建构数学模型
《义务教育数学课程标准(2011年版)》要求学生能从生活情境进中抽象出数量变化和变化规律并用符号来表示,这实际上就包含了模型思想。模型思想注重数学的应用,尤其是现实中的各种问题。
【案例】人教版《数学》五年级上册第一单元“解决问题例九”通过分段计费解决生活中坐计程车的数学问题。
1.在现实生活中抽象数学模型的策略
“分段计费”题目文字叙述对学生比较抽象、烦琐,理解起来困难较大,往往事倍功半。如果教育学生用符号表示数量关系进行建模,就会事半功倍。我采取“问题情境—建立模型—解释、应用扩展”展开教学。
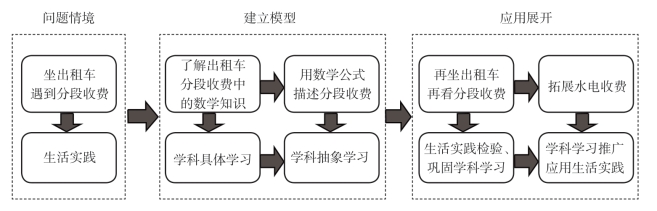
1)问题情境——体验生活,收集数据
学生坐过出租车,但对出租车如何计费并不清楚。课前布置体验作业:利用周末去坐一次出租车,并收好票据,了解出租车计费的方法,为建模提供丰富的感知认识。
课堂上,教师引导学生运用已有的数学知识理解这一生活现象。课始,请学生分享乘坐出租车的经历,谈谈了解到的出租车的计费标准。
师:从同学们的交流中可以看出出租车计费是分段计费的。分为哪几部分?
生1:分为两部分,第一部分3 km以内收费10元,超出3 km部分按1.8元/km。
生2:超出部分不足1 km按1 km计算。
师:不足1 km按1 km计算什么意思?
生1:即使是超出了0.2 km就要按1 km计算。
生2:也就是采用进一法来算路程。
通过交流引导,重点质疑理解,使重难点分段计费得以突破,使学生明确了解决问题的方向,有助于数学建模的形成。
2)建立模型——走进生活,抽象符号
除了捕捉生活现象,沟通数学知识与生活实际的联系,还要把生活中的问题逐步抽象成为数学符号,完成建模。在充分理解分段和进一法的基础上,发挥学生的主动性,放手让学生自主解决,充分交流,从而优化策略,最终形成解决问题的策略:分成两段计费,再合起来。
生1:分段计算
7+1.5×4=13(元)
生2:先假设再调整(加上少算的)
1.5×7=10.5(元)
7-1.5×3=2.5(元)
10.5+2.5=13(元)
生3:7+1.5×3.3(错)
……
师:你们能否用更简单的方式将计程车收费标准表示出来。
通过学生们的讨论得出
a=7+1.5×b (b为超过3 km部分)
师:你喜欢用哪种方式来知道收费标准?为什么?
通过正误的对比,不同方法的优化比较,使分段计费思路更加明确。在此基础上通过数学建模,让学生感受到数学的优点。
3)应用展开——回归生活,解决问题
数学建模重要的现实意义是要将数学模型应用于生活,并解决生活中的问题。为此,设计3个层面让学生展开应用:
(1)正反运用,检验模型。
找一个学生乘坐出租车的单据,让学生算出应付费用。
利用另一个同学所付费用,算出这位同学最远坐了多远。
用学生自己收集到的资料作为教学资源,运用a=7+1.5×b(b为超过3 km部分)来验证收费和行驶的里程数。使知识与生活联系得更加紧密,正反运用使学生对分段计费理解更加充分,让生活走进数学,数学模型应用于生活。
(2)拓展生活应用,发展模型。
新课程标准更多地强调学生用数学的眼光从生活中捕捉数学问题,探索数学规律,自主地解决生活中的实际问题,从而形成能力。为此,让学生解决水费、电费、邮费等生活中常见的收费,拓展生活应用,使分段计费模型得到了扩展。
(3)应用模型,感悟生活。
数学不仅仅要解决生活中的实际问题,而且还要去探寻这种现象的社会原因,感悟生活。为此,要求学生寻找生活中的分段计费,然后办一份小报(图1、图2)。在这次综合实践活动中,不但掌握了更复杂的分段计费模型,而且了解了更深层次的社会因素。

图1 “分段计费”小报(一)
图2 “分段计费”小报(二)
2.总结反思
小学数学的建模教学要引导学生捕捉生活现象,发现数学问题,将数学教学与生活接轨,构建数学模型,并运用数学模型去解决生活中的实际问题。打通学科学习与生活之间的壁垒,促使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到进步和发展。
