结合生活实际，创设生活化的探究活动
在传统的教学模式下，大多数学生处在较被动的地位，师生互动是教师和少数学生的互动，而学生在参与课堂教学的过程中都具有把握学习的主动权的权利与愿望，在图形与几何的教学中更要注重学生的参与性和体验性。感知动作同人的心理活动密切联系着，感知体验越深刻，动作记忆保留的时间更长久，让学生参与观察、比较、动手操作活动中，有利于学生理解几何概念和图形的特征。
（一）鼓励引导学生结合生活经验大胆猜想
在开始探究活动前，教师可设置一个分析问题的环节能够帮助学生理清探究思路。根据皮亚杰的认知发展理论，学生新知的学习是一个同化和顺应的过程，学生在走进课堂之前已积累了丰富的生活经验，他们能根据已有的生活经验进行描述和猜测，经历猜想和表达的过程唤起原有经验是构建认知图式的第一步。
例如，在“长、正方体表面积和体积练习”一课中，根据学生的生活和学习经验，问学生现有3种材料：铁丝、纸板、木料，你能想象用这些材料做成同样大小的长方体学具各需要多少材料吗？（接头处忽略不计）通过“选择不同材料制作相同的长方体学具”这一活动就是对棱长和、表面积和体积进行复习。
接下来，老师可设计板书点→线→面→体，体现棱长和、表面积和体积三者之间的维度关系，让学生领悟解决问题不能呆板，需要根据具体情况大胆猜想，具体分析找到解决问题的方法，结合问题思考三者情况的几何图形，进而培养空间思维。
又如，在“圆的周长”一课中，设计了让学生猜测周长和直径倍数关系的教学环节：
（1）初步猜测：圆的周长和直径有怎样的关系。
（2）数形结合猜测：数学研究需要大胆猜测。我们的猜测既要大胆更要有依据。看看下面这幅图能给你什么启示。
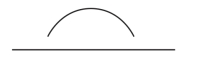
（课件）出示：
（3）比比圆周长的一半和一条直径有什么关系。谁长？
（4）整圆：那整圆的周长和两条直径比呢？（圆的周长大于直径的2倍）
（5）出示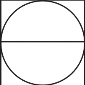
，你发现了什么？
①圆装在了正方形里面，你知道了什么？（可见圆的周长一定比正方形的周长小）
②再看（出现直径），正方形的周长与直径有什么关系？（正方形的周长是直径的4倍）
③也就是说，直径的4倍就是正方形的周长。
④（手势）那圆的周长比直径的4倍要（小）。
（6）根据这两幅图，可很肯定地说，圆的周长在它直径2倍和4倍之间。
鼓励学生结合生活经验和旧知对新知进行大胆猜想，培养学生的想象能力和空间思维。
（二）设计动手操作活动，借助生活经验验证猜想
在教学中，教师应为学生多设计动手操作的活动，并提供较充分的动手操作的时间和空间，让学生自己体会知识的发生过程。开展动手操作能提高学生的学习积极性，学习不再是被动地听取老师介绍知识的产生过程，而是自己动手去发现。在进行操作的过程中，学生手脑并用，注意力也相当集中，这样主动的学习更能让学生体会到学习的成就感和满足感。
例如，在“认识平行四边形”一课中，学生对平行四边形以及它的特征进行学习，可通过动手操作、观察和比较等方法。教师可组织学生开展实践操作活动，通过拼、折等方式来组合图形，这样一方面将平行四边形的特征进行了验证，加强了对平行四边形特征的理解，另一方面老师可通过学生动手操作的过程了解学生对知识的掌握程度，以调整下一环节的教学方法，帮助学生发展空间观念，以对平行四边形建立准确感知。
又如，在“圆的周长”一课中，设计了让学生动手测量、计算周长和直径倍数关系的教学环节：
师：圆的周长是它直径的几倍呢？要得到准确的倍数你有什么办法？
（课件）活动：实验步骤。
（1）先量出圆的周长和直径并记录。
（2）算算圆的周长是它直径的几倍。
生实验操作后汇报。
师小结：刚才同学们算出了周长是直径的几倍。其实，就是周长/直径的比值。
学生在大胆猜想后要让学生动手操作，借助生活经验验证猜想，从而得出结论。因此，培养了学生科学严谨的学习态度。
（三）在活动中观察比较，发展学生的空间想象能力
在“图形与几何”板块教学中，小学阶段学生的空间想象需要具体实物的支持。因此，在教学中要符合学生的思维特点和认知方式，可让学生对实物进行观察、比对。学生在直观的感受中，能发展对图形的观察能力和空间感，帮助学生感知和深入体会几何概念。
例如，在三年级上册“周长的认识”一课中，为学生提供大量的感性材料，组织“描、摸、围、数、量”等活动，经历测量与相加，图形长度到线段长度，曲线到直线，不规则到规则，借助直观线绳，把不同图形轮廓、外形、边线都变成一条线段，让学生进一步感受到周长其实就是长度，在动手操作体验中建构周长的表象，让操作活动概括上升到理性层面，突显概念本质属性。
又如，在“圆的认识”一课中，探索半径和直径的关系中设计了这样的活动环节：
活动：把一个圆，沿着直径折一折、画一画、量一量，会有什么发现？
温馨提示：可从直径和半径的条数、长度去研究发现。
要求：
（1）自己动手操作。
（2）小组内交流，并想办法验证。
（3）组长做好记录。
结论一：半径无数条。
验证：画、折。
结论二：所有半径的长度相等。
验证：量、折、比。
结论三：直径无数条。
验证：画、折。
结论四：圆是轴对称图形，它的对称轴就是直径所在的直线。
结论五：同圆或等圆中，所有直径长度相等。
验证：量、折、概念。
关系d=2r。
验证：量、折、画。
学生通过折一折、画一画、量一量的操作活动，通过观察比较可发现半径无数条，所有半径的长度相等，直径无数条，圆是轴对称图形，它的对称轴就是直径所在的直线，直径和半径的关系d=2r。因此，发展了学生的空间想象能力。