14.2.2 城市房地产投资风险概率分析的主要方法
投资风险概率分析主要有期望值法和蒙特卡罗模拟法两种分析方法。
1.概率分析的期望值法
概率分析的期望值法,就是求出项目投资净现值大于等于零的累计概率,并以此分析项目投资是否可行以及承担风险性大小的一种方法。
采用期望值法进行概率分析,一般需要遵循以下步骤:
(1)选用净现值作为分析对象,并分析选定与之有关的主要不确定性因素。
(2)按照穷举互斥原则,确定各不确定性因素可能发生的状态或变化范围。
(3)分别计算各不确定性因素每种情况下发生的概率。各不确定性因素在每种情况下的概率,必须小于等于1、大于等于0,且所有可能发生情况的概率之和必须等于1。
(4)分别计算各可能发生情况下的净现值,包括各年净现值期望值和整个项目周期净现值的期望值。项目净现值期望值大于零,则项目投资可行;否则,项目投资就不可行。
(5)计算各年净现值标准差、整个项目周期净现值的标准差或标准差系数。
净现值标准差在一定程度上能够说明项目风险的大小。但由于净现值标准差的大小受净现值期望值影响很大,两者基本上呈同向变动,因此,单纯以净现值标准差的大小衡量项目风险性高低,有时会得出不正确的结论。为此需要消除净现值期望值大小的影响,计算整个项目周期的标准差系数。其计算公式为:
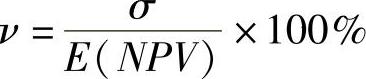
式中,ν为标准差系数。一般来说,ν越小,项目的相对风险就越小;反之,项目的相对风险就越大。依据净现值期望值、净现值标准差和标准差系数,可以用来选择投资方案。判断投资方案优劣的标准是:期望值相同、标准差小的方案为优;标准差相同、期望值大的方案为优;标准差系数小的方案为优。
(6)计算净现值大于或等于零时的累计概率。累计概率值越大,项目投资风险就越小。
(7)对以上分析结果作综合评价,说明投资项目是否可行及承担风险性大小。
期望值法进行概率分析,需要利用概率树或决策树分析法。该方法是一种用树形图来描述各方案在未来收益的计算、比较以及选择的方法,其决策是以期望值为标准的。整个概率树或决策树由决策结点、方案分枝、状态结点、概率分枝和结果点五个要素构成。图14-1是概率树的基本结构。图中,方案分析结果从左到右依次展开,逐步分析事件的发生与发展,好像一棵不断分枝的树,用树形图作为可能状况及结果的完整关系表示图。把决策过程引入概率树就是决策树。根据决策树决策的计算过程是,把概率树折叠,即从左到右的方向进行计算,每到一个决策点,选取具有最大利益或最小损失(期望值)的行动方案,再把决策树转回到前一决策点,以此类推,最终完成决策活动。
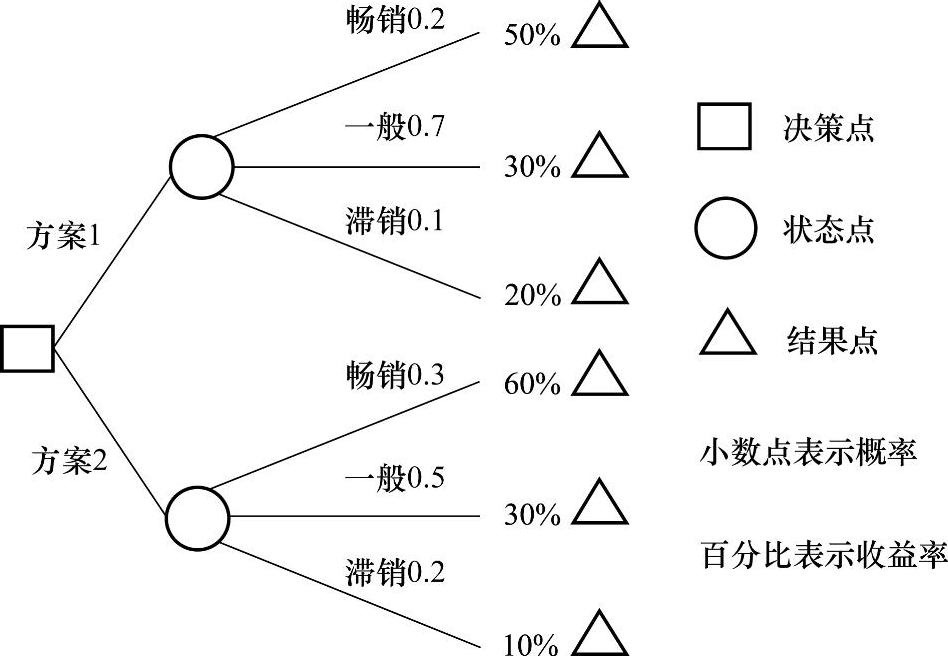
图14-1 概率树的基本结构
一般来说,概率树分析法使大规模或复杂问题分解成小的子问题,这些小的子问题可以分别加以解决,然后重新组织起来,当问题具有某种可以肯定的结果时,这种分析方法是很有用的。
[例14-1] 某投资者以25万元购买了一个商铺2年的经营权。第1年净现金流量可能为22万元、18万元和14万元。概率分别为0.2、0.6和0.2。第2年净现金流量可能为28万元、22万元和16万元。概率分别为0.15、0.7和0.15。若折现率为10%,试分析购买该商铺的投资是否可行。
解:
本题可用Microsoft Excel软件来自动计算,并进行分析,如表14-1所示。
表14-1 房地产投资项目可行性分析表 (单位:万元)
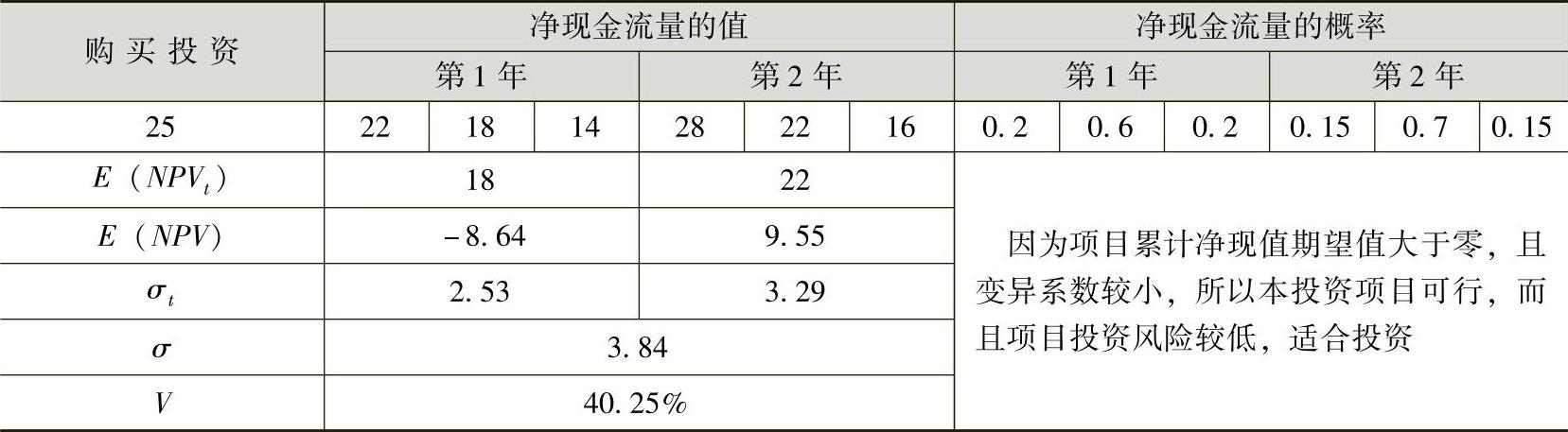
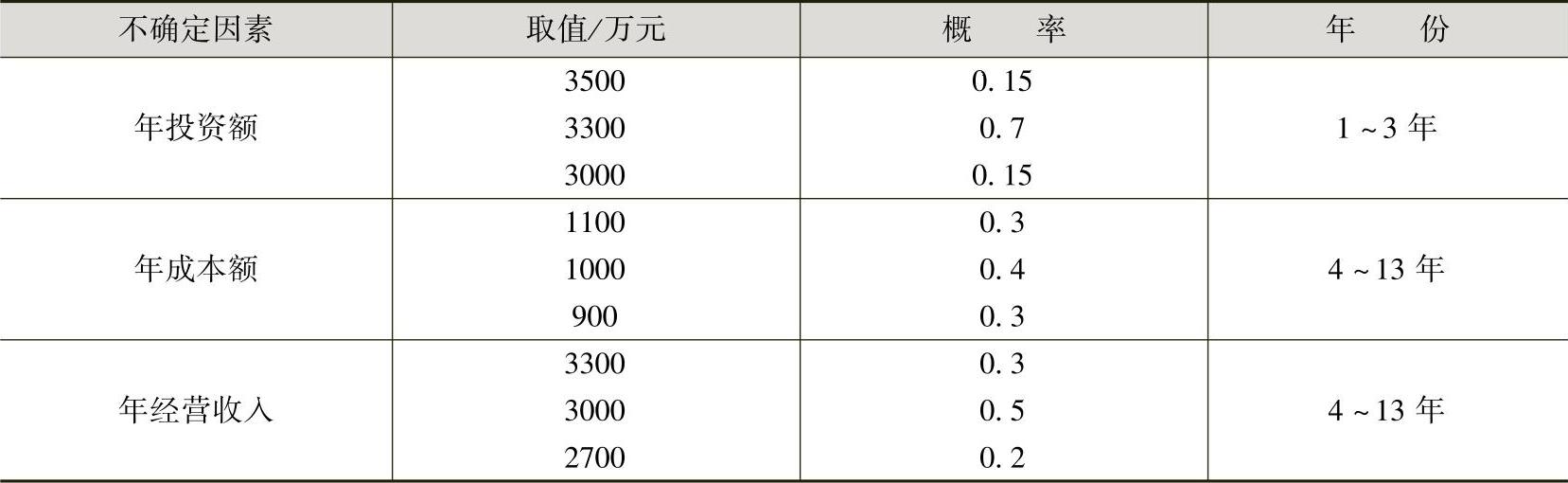
[例14-2] 某项目的有关经济数据如表14-2所示。其中建设期为3年,每年投资的可能值为3500万元、3300万元、3000万元。经营期为10年,每年的成本值为1100万元、1000万元、900万元,每年的经营收入可能值为3300万元、3000万元、2700万元。假设折现率为10%,净转售收入为2000万元。试用期望值法对该投资项目进行风险的概率分析。
表14-2 项目投资经营有关经济数据
解:
(1)列出现金流量、概率序列。具体如图14-2所示。
(2)用资金时间价值和概率有关计算公式求出现金流量序列的现值、净现值及其相应的概率。具体如图14-3所示。
图14-3中净现值的概率用概率乘法公式计算,等于现值序列各概率值的乘积。加权净现值等于净现值和其概率的乘积。
(3)求净现值的期望值。它等于各加权净现值之和。本例计算结果为1202万元。
(4)把净现值从小到大按顺序排列成表,并求出各净现值累计概率(见表14-3),还可作出净现值累计概率图(略)。
表14-3 项目投资的净现值及其累计概率
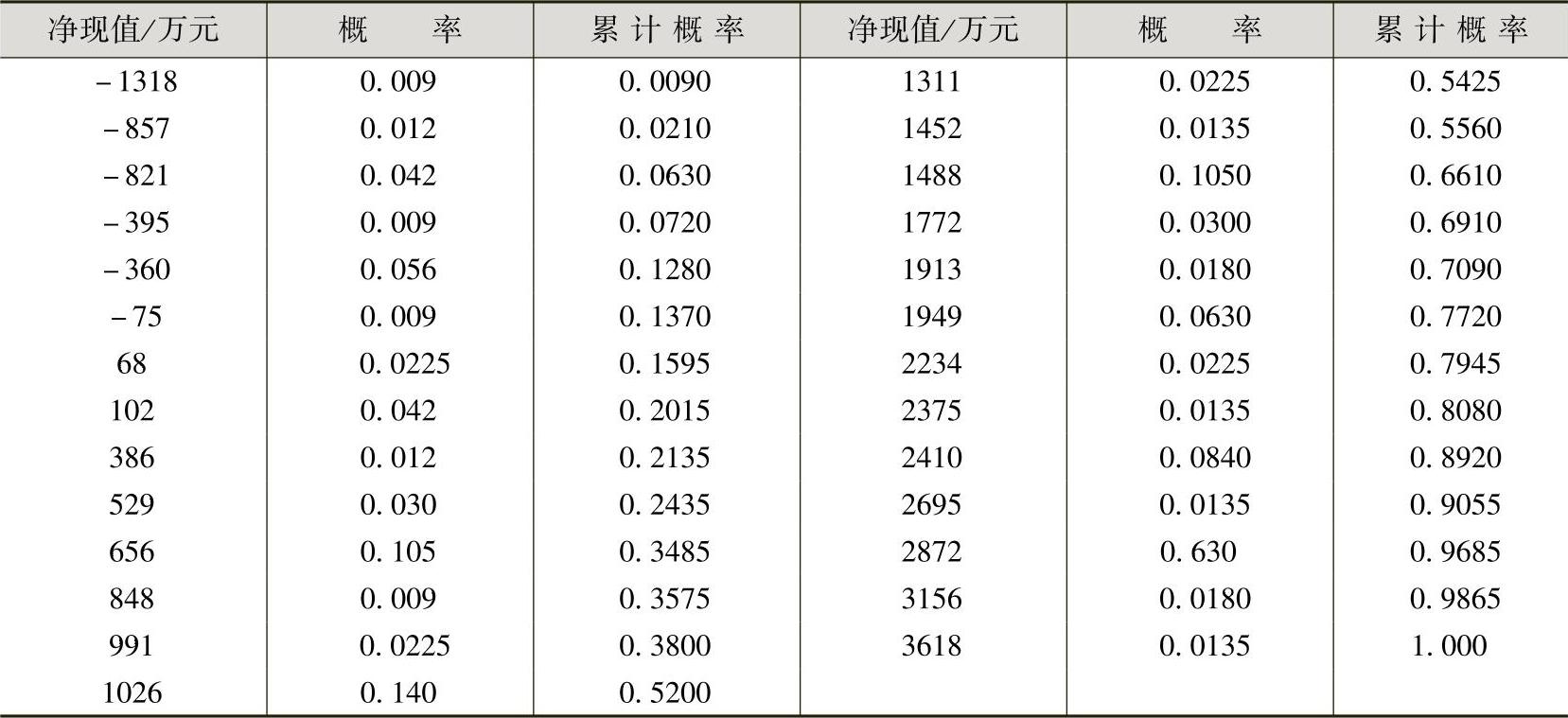
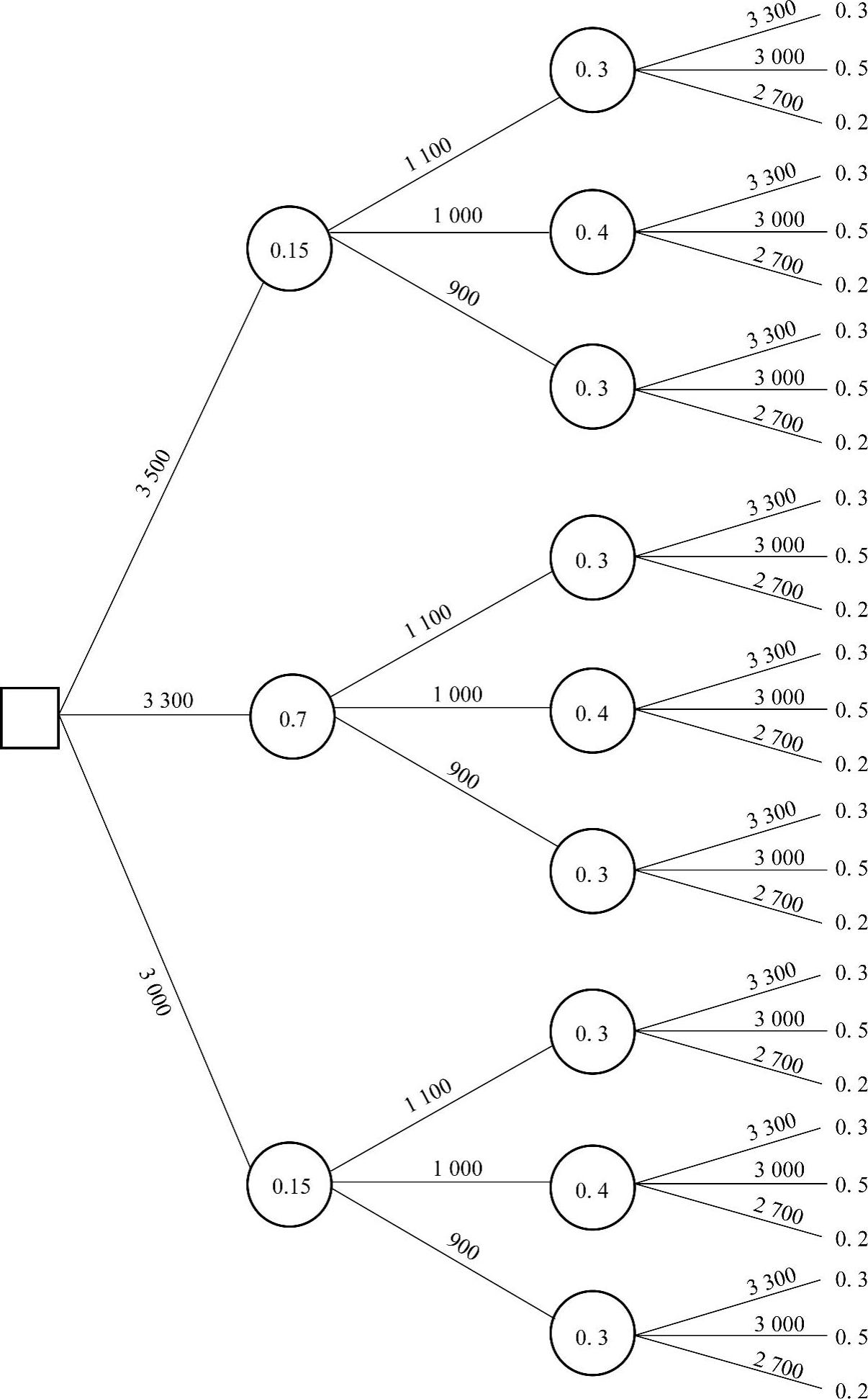
图14-2 项目现金流量及其概率分布(单位:万元)
(5)求净现值小于零的概率。从表14-3中可知:
P(NPV<-75)=0.1370,P(NPV<68)=0.1595
使用插值法可以求出净现值小于零的概率:
P(NPV<0)=0.1370+(0.1595-0.1370)×75/(75+68)=0.1488
根据以上计算结果可以得到结论:本项目的净现值期望值E(NPV)=1202万元,但存在净现值小于零的可能性为14.88%的风险。至于这一项目是否采纳,需看投资者是否愿意为了取得1202万元的净现值期望值而去冒14.88%的亏损可能性的风险。但一般来说,本项目投资的风险并不大,是一个可以接受的可行的投资项目。
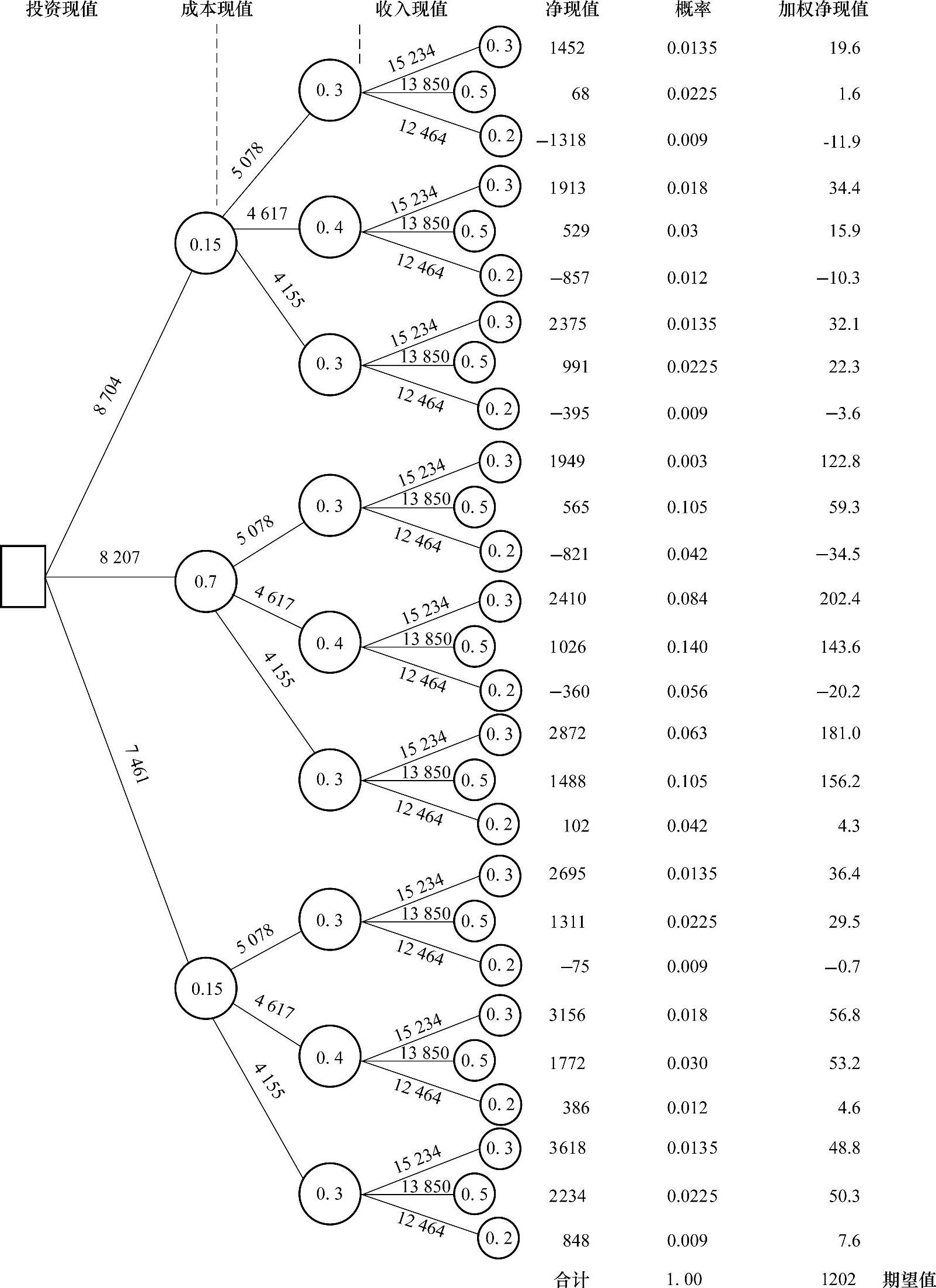
图14-3 项目投资经营的现值、净现值及其相应的概率(单位:万元)
实际投资活动中,每个投资项目都有若干个随机变量,每个随机变量又可能有若干个取值,这种情况下,运用期望值法进行分析决策就显得非常复杂和困难。即使运用计算机,要将所有可能的情况都计算一遍也是很困难的,需要的时间和费用相当大。所以,就需要采用蒙特卡罗模拟法。
2.概率分析的蒙特卡罗模拟法
蒙特卡罗模拟法,又称为统计实验法或随机模拟法。该方法运用蒙特卡罗模拟的统计功能,自动对项目评估中涉及的每个变量的数值进行选择和组合。在大型的房地产项目建设周期内,市场、利率、通货膨胀和技术进步等情况都会不同程度的发生变化。所以,在这种情况下,要综合各项影响因素,运用概率树分析法对城市房地产投资项目作出较为准确的风险估算是相当困难的。而蒙特卡罗模拟法正好可以解决这个困难,分析人员可以输入各种可能发生情况的数据,蒙特卡罗模型就能够随机模拟各种变量间的动态关系,从而使人们掌握输出量的概率分布,最终解决某些具有不确定性的复杂问题。使用蒙特卡罗模拟法的过程中需要反复的取值,随着取值次数的增多,其预计精度也逐渐增高。由于需要大量反复的计算,一般均用计算机来完成。
蒙特卡罗模拟法的步骤大致如下:
(1)分析每一可变因素的可能变化及其概率分布,这可以用简单的概率表来完成。
(2)通过模拟试验随机选取各随机变量的值,并使选择的随机值符合各自的概率分布,为此可使用随机数或直接用计算机求出随机数。
(3)反复重复以上步骤,进行多次模拟实验,即可求出开发项目各项经济效益指标的概率分布或其他特征值。
[例14-3] 某开发商拟在其以20万美元购得的一块土地上开发一栋写字楼,规划建筑面积是2000m2,建造成本是200美元/m2,项目的准备期为3个月、建造期为12个月,第4个月到第15个月投入的建造成本分别占总建筑成本的3.8%、4.7%、5.8%、6.9%、8.6%、10.3%、12.7%、13.5%、11.9%、8.5%、6.8%和6.5%。预计项目投入使用后年租金收入为6万美元,贷款利率为15%。试使用蒙特卡罗模拟法进行风险分析。
解:
首先,需要确定每一个可变因素的变化范围及概率分布状况,如表14-4所示。
表14-4 可变因素及其变动情况
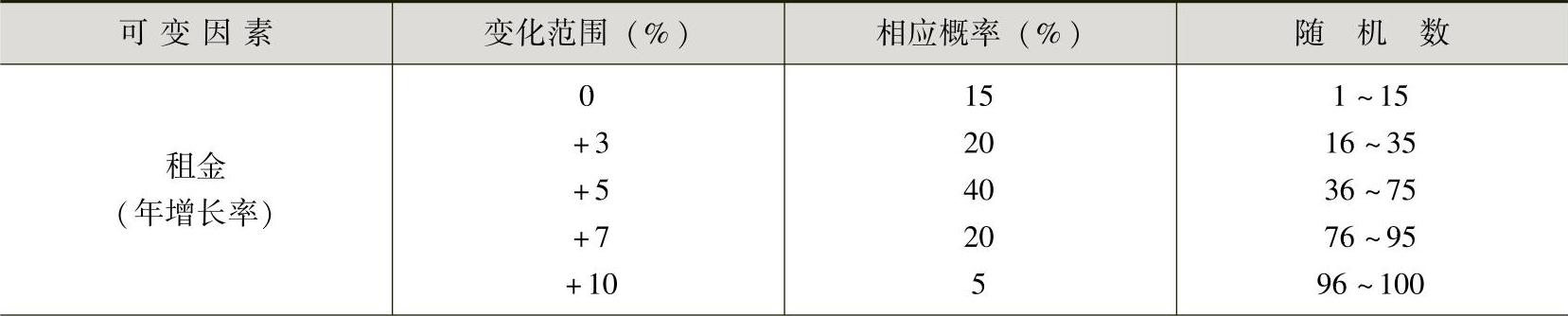
(续)
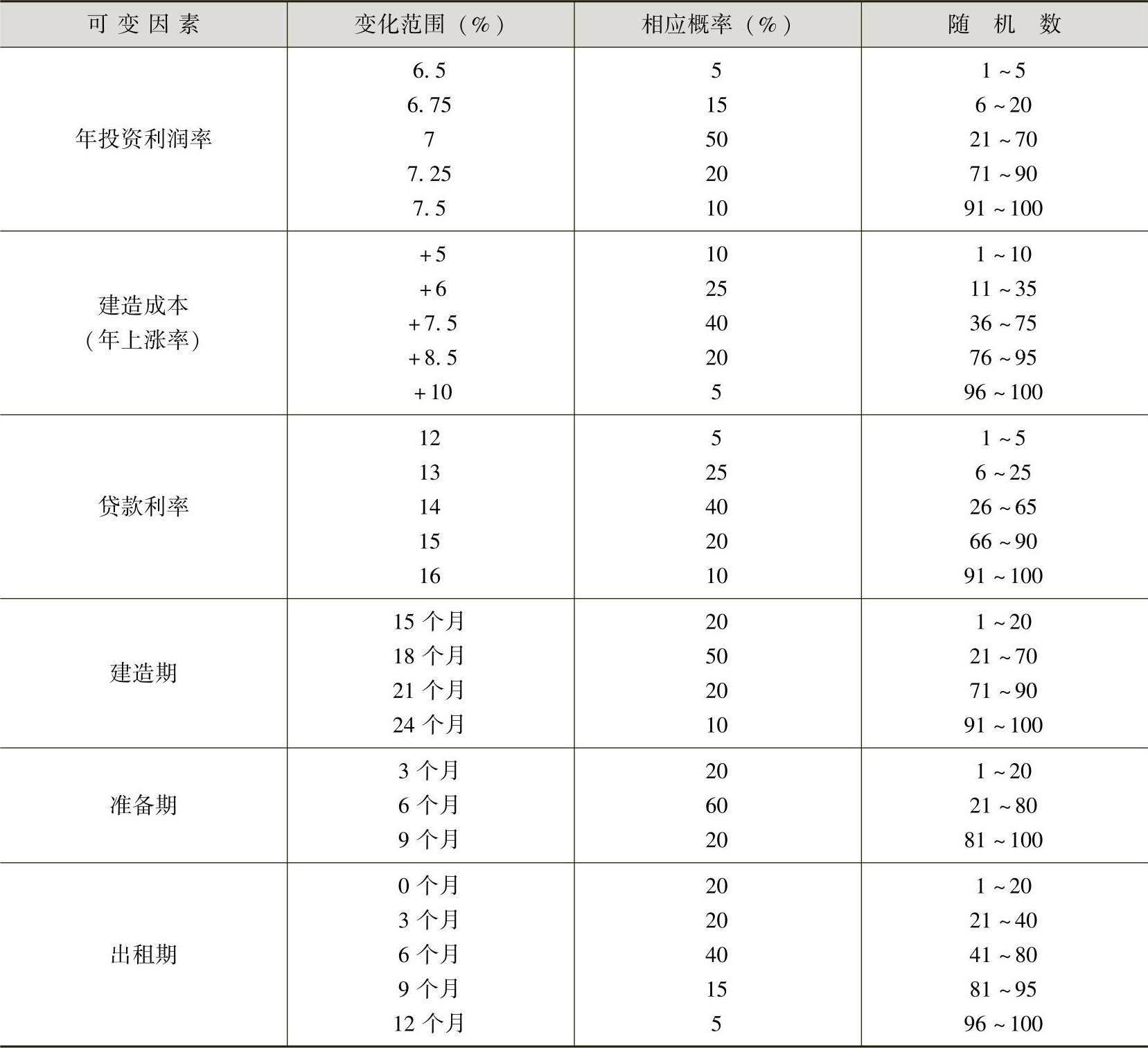
在分析完每一因素的概率分布以后,就要根据模型中各个随机变量的分布,在计算机上产生随机数。例如,使用计算机求出租金增长率的随机数是22,则根据表14-4可知,该随机数介于16~35之间,对应的年租金增长率为+3%。依次对其他的因素产生的随机数分别是53、14、80、42、77、68,则相应各因素的值如表14-5所示。
表14-5 模拟试验随机选取的变量值

上表是模拟一次产生的结果。
利用抽样法得到数据,多次重复,进行多次模拟试验,即可得出开发项目各项效益指标的概率分布。根据表14-4的概率假设,对本例模拟1000次的结果如表14-6所示。
表14-6 1000次模拟试验下的分析结果
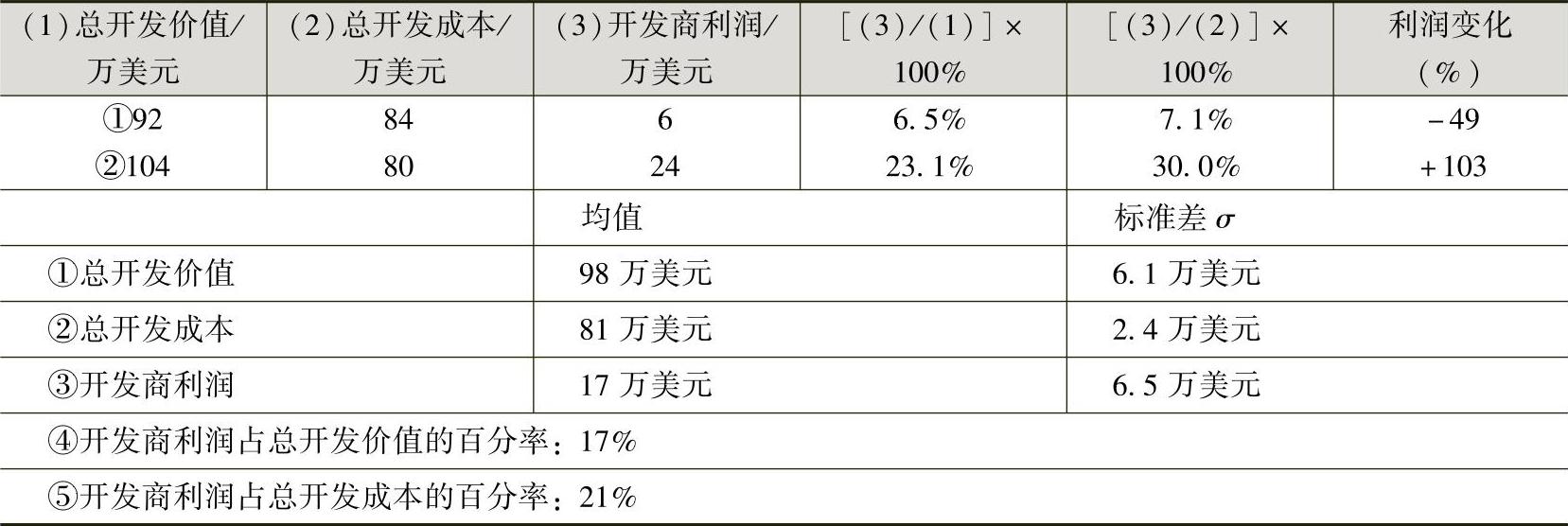
假设开发商利润服从正态分布,则开发商利润有95%的可能(±2σ)落在4万~30万美元。
这种风险分析的结果是否被开发商接受,取决于开发商对待风险的态度和其接受风险的标准。蒙特卡罗模拟法为开发商提供了更加充分、精确的数据进行风险分析。
当对一个项目的风险可以主观判断,但又难于定量计算出来时,就可以应用蒙特卡罗模拟法进行分析。这种分析方法比较具有洞察力。但由于应用这种方法进行估算时需要准确估计各因素的变化范围以及变化概率,而实际操作中许多信息又是不充分的,这就给分析过程带来了比较大的麻烦。虽然如此,蒙特卡罗模拟法在近几十年的城市房地产投资分析及评估中也被国内外学者广泛应用,相当多的城市房地产投资项目都使用此法进行风险评估。
