1.2.1　经典李群方法

1.2.1　经典李群方法

下面将简要地介绍对于给定的偏微分方程，如何寻求偏微分方程的李对称.

首先，考虑一般的n维偏微分方程系统（包含p个自变量、q个因变量）[44-50]

这里 x=（x1，x2，…，xp），u=（u1，u2，…，uq），最高阶导数为n。考虑单参数李变换群

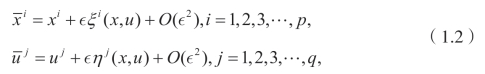
这里∊是群参数。上面变换群所对应的无穷小生成元可以表示为

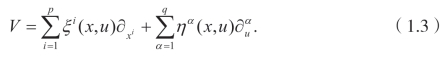
利用微分方程的不变性准则可以得到不变条件

这里 ∆v（x，u（n））=0，pr（n）V 是无穷小生成元的n阶延拓

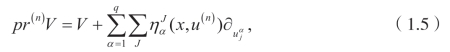
并且J=（j1，j2，...，jk），1≤jk≤p，1≤k≤n。n阶延拓的系数函数由下式给出

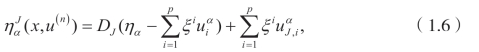
这里。得到无穷小生成元的系数之后，就可以得到相应的无穷小生成元，当把无穷小生成元确定后，通过求解下述李方程：

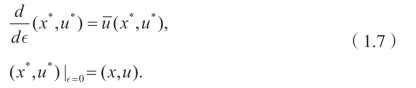
就可以求出相应的单参数群