3.2.2　Painleve 分析

3.2.2　Painleve 分析

类似于三阶Burgers 方程，按照 Laurent 级数展开 u（x，t）

将

代入（3.72），并且对领头项分析，可以得到 α=−1，u0=ϕx，u0=2ϕx，或者u0=3ϕx。

对于 u0=ϕx，得到

可以发现共振项出现在

因此可以说，四阶Burgers 方程具有Painleve 性质 j=1，2，4。为了寻找Bäcklund变换，考虑下面的有限展开，并且假定(https://www.daowen.com)

因此，我们可以得到下面的 Bäcklund 变换

尤其是当u1=0时，可以得到著名的Cole-Hopf 变换

并且得到下面的四阶线性的偏微分方程

此外，需要注意的是 u0=ϕx是一个非局域对称。另一方面，将（3.75）代入（3.72），可以得到

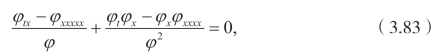
也就是说 ϕt=ϕxxxx.换句话说，基于Cole-Hopf 变换，将四阶Burgers 方程变换成四阶线性偏微分方程。下一小节可以发现，基于对称，该方程转换成同样的四阶线性偏微分方程。