4.2.2 李对称群分析
2026年01月14日
4.2.2 李对称群分析
这一小节,依然是基于李对称分析考虑该方程。基于李对称分析方法,假定下面的无穷小变换,
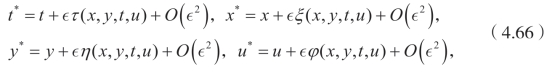
相应的向量场是
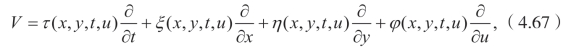
目的是求向量场的系数函数τ(x,y,t,u),ξ(x,y,t,u),η(x,y,t,u) 和 ϕ(x,y,t,u)。
此时,V需要满足下面的李对称条件
![]()
这里∆1=ut+auux+b(uxxx+uyyy)+c(uxyy+uxxy)=0。
利用三阶延拓公式,可以得到
![]()
这里
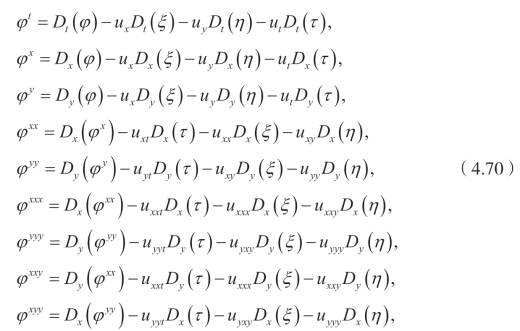
Di依然是全导数算子
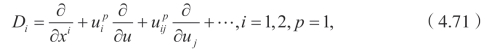
这里(x1,x2,x3)=(t,x,y),(u1)=(u)。
考虑到李对称方法,可以推出
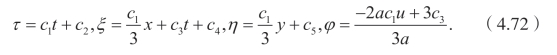
这样一来,对称代数由下面的五个向量场构成:
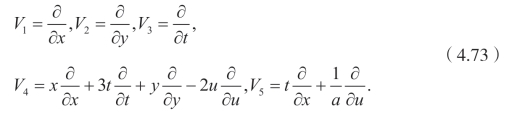
容易验证,对称算子构成了封闭的李代数。表1给出了它们的交换关系。这里[Vi,Vj]是交换李代数[48]:
表1 李代数的交换表
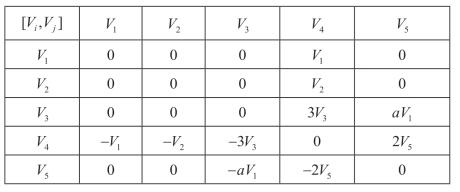
[Vi,Vj]=ViVj−VjVi.(https://www.daowen.com)
可以发现,它们构成了五维李代数。为了从已知解去得到新解,要从相关的对称去发现李对称群。为了得到李对称群,需要求解下面的初值问题:
![]()
这里 ∊ 是参数,并且
![]()
所以我们可以得到李对称群
![]()
选择不同的ξ,τ η,和ϕ,可以得到下面的群
g1:(x+ε,y,t,u),
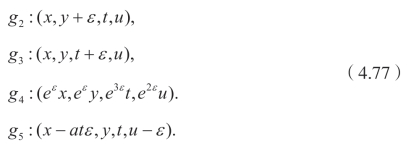
对称群g1,g2和g3表明方程的时空不变性,g4是著名的标量对称群,利用上面的不变群gi(i=1,…4),可以得到相应的新解
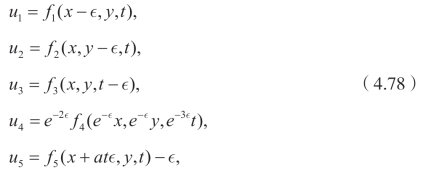
这里∊ 是任意的实参数。
如果取文献[104]里的单孤立子解作为种子解,
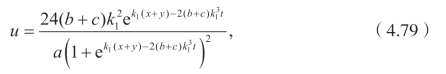
利用不变群g5,可以得到下面的新解
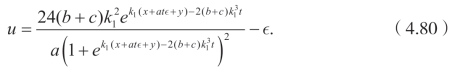
如果取文献[104]里的奇异孤立子解作为种子解,
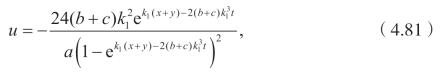
再次利用不变群g5,可以得到新解如下
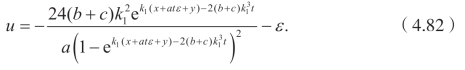
显而易见,选择任意的常数,可以得到大量丰富的新解。
注记 利用已知解,可以得到大量的新解,从而对于[104]来说,利用他们得到的解,我们可以得到大量的新解,推广了相应的结果。
