3.1.5　势方程的约化和相似解

3.1.5　势方程的约化和相似解

这一小节，考虑势方程（3.16）的不变解以及约化。考虑下述情况

情况1.X1.对于这种情况，得到不变量是 ξ=t，得到平凡解 v=c1。

情况2.X2.对于此种情况，得到不变量是ξ=x，而且可以得到下述方程

对于该方程，得到积分因子

这里C1，C2，C3和C4是任意常数。

这样一来，（3.39）可以转化成下面的情况：

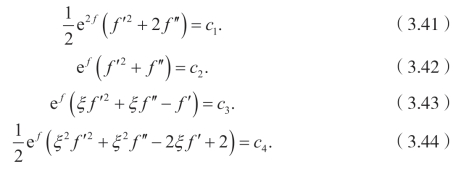
求解（3.41），得到

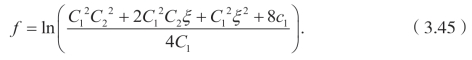
将（3.45）代入（3.42），（3.43），（3.44），可以得到

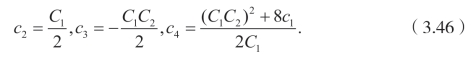
情况3.λX1+X2.对于线性组合，不变量是ξ=x−λt，不变函数 f（ξ），可以得到下面的方程

对于这种情况，可以得到下面的积分因子

这里C1，C2，C3，C4是任意常数。

于是有下面的式子：

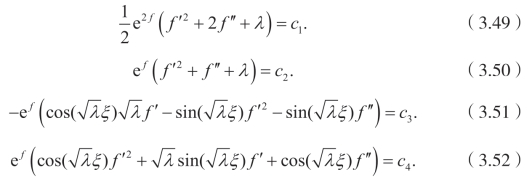
求解（3.49），得到

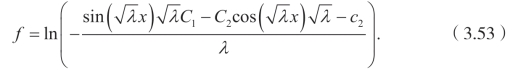
将（3.53）代入（3.50），（3.51）和（3.52），可以得到

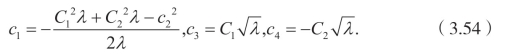
情况4.X4.对于这种情况，不变量和不变函数分别是和 f（ξ），并且得到下述方程

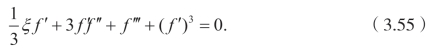
用相似的步骤，可以得到积分因子

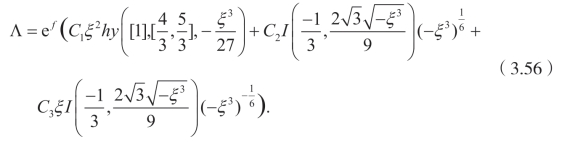
因此，有

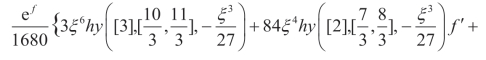
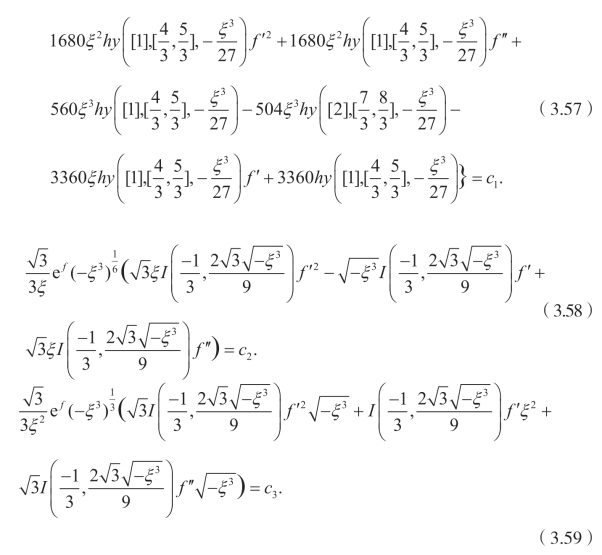
求解（3.58），可以得到

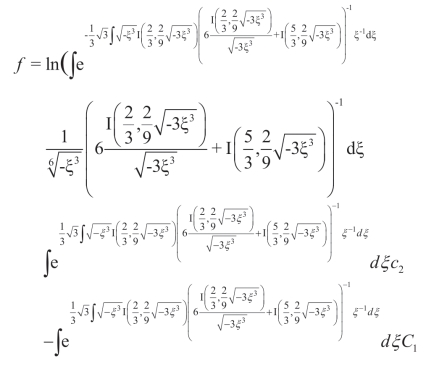
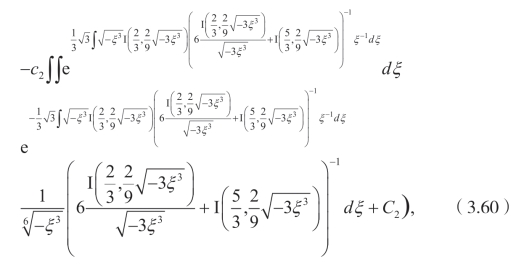
这里 I 是第一类 Bessel 函数，而hy 是超越函数。