3.2.4　势方程的李对称、非线性自治性和守恒律

3.2.4　势方程的李对称、非线性自治性和守恒律

3.2.4.1　李对称分析

势方程（3.85）具有下面的点对称

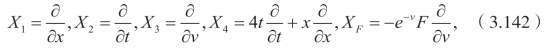
这里 F=F（x，t），并且 F 是Ft−Fxxxx=0的一个解。

3.2.4.2　非线性自治性

定义 3.2.1 [72，100]（3.85）就说是非线性自治的，如果对于一些任意的函数 ϕ（x，t，v）≠0，满足

这里 λ 为待定系数并且F* 是伴随方程。

定理 3.2.1 [72，100]每一个李点对称，Lie-Bäcklund 对称和非局部对称，守恒量由下述公式给定

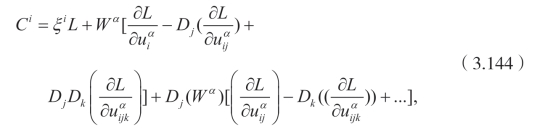
这里Wα=ηα−ξj uαj。

对于势方程（3.85]）的伴随方程，有

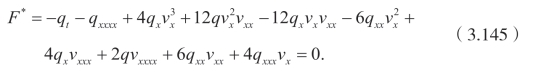(https://www.daowen.com)

容易验证势方程不是自治的，因为将v代替q以后，得不到原方程。现在为了寻找显式形式的 ϕ（x，t，v）≠0

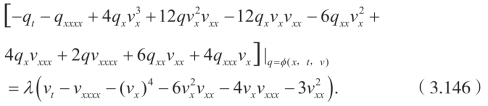
令 q=ϕ（t，x，v），得到

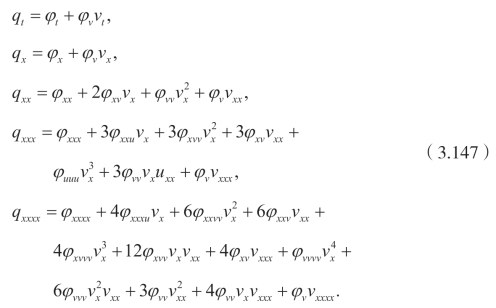
将（3.147）代入（3.146），从vt的系数可以得到，

令v及其导数项等于零，可以得到

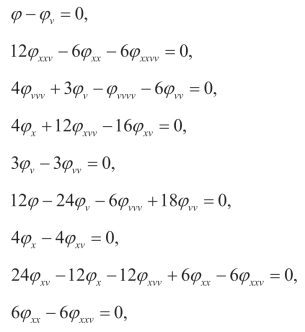
解这些方程，可以得到

这里a，b，c 和d都是常数。因此我们有下面的定理

定理 3.2.2 如果 q=ϕ并且ϕ由（3.150）确定则势方程是非线性自治的。