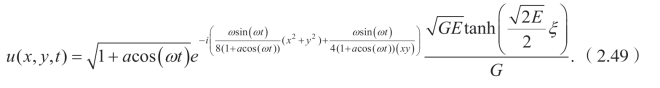2.4　相似变换

2.4　相似变换

这一小节，考虑一般的情况，首先基于一个相似变换，将变系数（2+1）非线性薛定谔方程约化成稳态的立方非线性薛定谔方程

这里U=U（ξ）和ξ=ξ（x，y，t） 是实函数，E表示该方程的特征值，而G是常数。为了得到（2.23）和（2.1）之间的关系，用下面的相似变换[77-79]

将（2.24）代入（2.1），可以得到

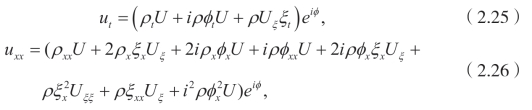
将它们代入（2.1），并且分离实部和虚部，得到

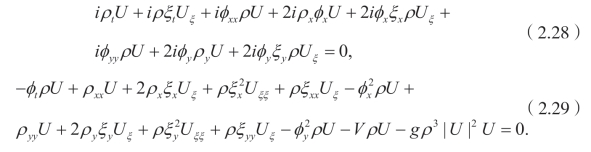
令 U 以及不同的导数项系数等于零，可以得到

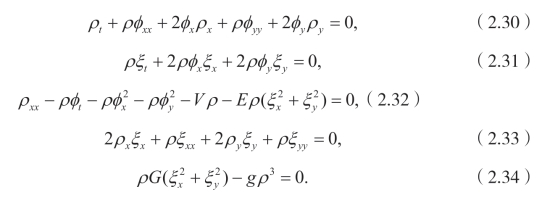
求解（2.32）和（2.34），得到

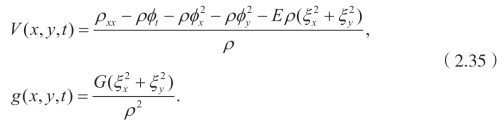
考虑剩下的其他的方程，可以得

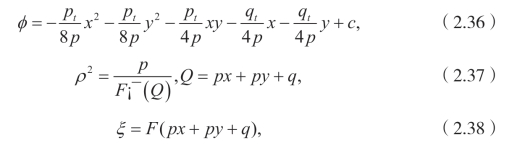
这里 p，q和 c 是t的任意函数。

这样一来，选择合适的函数p（t），q（t），F（px+py+q），就可以得到g（t，x，y），V（t，x，y）。自然而然地可以得到许多有趣的结果。

因为（2.23）有大量的解，得到

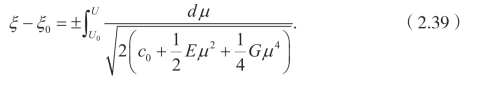
这里ξ0 和 c0 是积分常数。因此，可以得到（2.1）的精确解：

这里

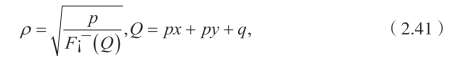
和

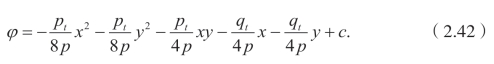
此外，

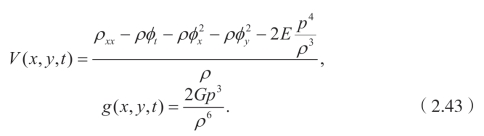
很明显（2.23）有一个亮孤立子解，

这里 E=−κ2 和G=−2κ2，并且有一个暗孤立子解，

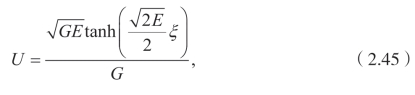
其中E，G 是正数。

下一小节，考虑不同的非线性G 和势函数V（t，x，y）。

例子

首先，选择ρ（x，y，t）=，对于这种情况，可以得到 g（x，y，t）=2G 和ξ=F（Q）=Q=p（x+y）+q。因此有

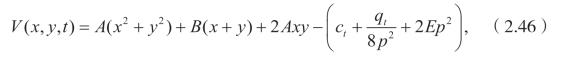
这里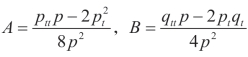。选择不同的p，q 和c 可以得到大量的解。

现在，令

这里 和 ω ∈R。此时（2.40）是关于t的三角函数，所以它们是呼吸孤立波解。这样，可以得到（2.1）的解

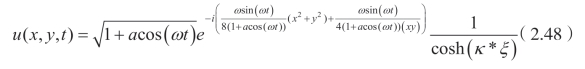
和