6.2　（2+1）-维sine-Gordon 和sinh-Gordon 方程的导出

6.2　（2+1）-维sine-Gordon 和sinh-Gordon 方程的导出

众所周知，AKNS 系统[10]是经典可积系统之一，该系统可以推导出许多著名的方程，比如 KdV 方程、mKdV 方程、非线性薛定谔方程、Burgers 方程、（1+1）-维sine-Gordon 方程等。基于AKNS 系统，考虑下面的（2+1）-维零曲率方程[10，122，123]

这里

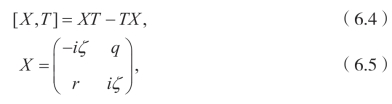
且

利用相容性条件，令特征值是关于时间不变的，也就是说，ζt=0。将方程（6.5）和方程（6.6）代入方程（6.3），得到下面的方程

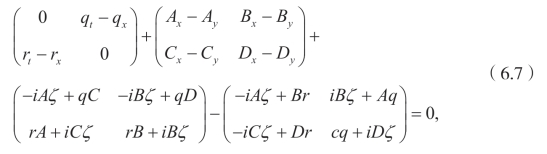
换句话说，

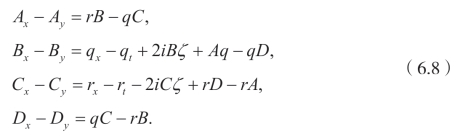
从第一个和最后一个方程，可以得到D=−A。因此，方程（6.8）变成

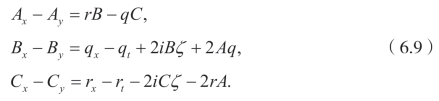
下面的问题是如何求解方程（6.9）。根据文献[10]，将 A，B，C，D 展成关于特征值ζ的有限截断形式，正的情况已经有许多论文研究过，因此这里考虑负的情况。利用下面的展开公式

将方程（6.10）代入方程（6.9）中，得到

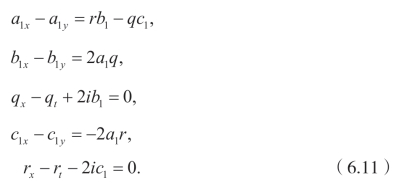
现在考虑下面的特殊情况

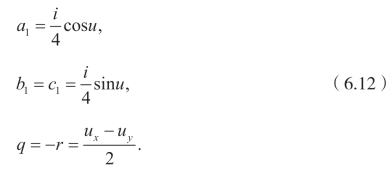
这样一来，得到（2+1）-维sine-Gordon 方程

类似考虑下面特殊情况：

得到（2+1）-维sinh-Gordon 方程

注记：1．自然而然地可以得到（2+1）-维双sine-Gordon 方程和双sinh-Gordon 方程

uxx−uxy−uxt+uyt=sinu+sin2u,

uxx−uxy−uxt+uyt=sinhu+sinh2u.

2．再变换ξ=x+y+t，η=y，τ=t，方程（6.13）和（6.15）可以约化成（1+1）-维的情况 Uητ=sinU 和Uητ=sinhU。