1.2.2 非经典李群方法
2026年01月14日
1.2.2 非经典李群方法
非经典对称方法是由Bluman 和Cole[40] 于1969年在研究一维热传导方程时提出,该方法是在经典李群方法的基础之上,通过向量场及其延拓来求得。与经典李对称方法相比,增加了不变曲面条件为零的条件,也就是说,要求在不变曲面条件和微分方程同时为零的公共解集上寻找相应的单参数群。表面上看,虽然只是增加了不变曲面条件也为零的条件,但是,在求解无穷小生成元的时候,难度会大大增加,因为此时已经不再是线性方程组,而是非线性、超定的偏微分方程组。就单个非线性偏微分方程来说,求解已经够困难,那么对于非线性偏微分方程组来说,自然更为困难,更为复杂。在求解这样的超定方程组的时候,能得到更丰富的解和更丰富的对称.
例如,对于如下(1+1)-维非线性偏微分方程[44-50]:
![]()
考虑单参数李变换群
![]()
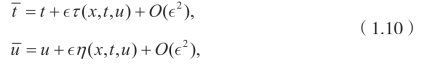 (https://www.daowen.com)
(https://www.daowen.com)
这里∊是群参数。相应的无穷小生成元可以表示为
![]()
此时的不变条件为
![]()
这里 ∆1=ξux+τut−u。这是与经典李群方法唯一区别的地方,其余过程与经典李群方法类似,就是求无穷小生成元。
