3.1.2　Painleve 分析

3.1.2　Painleve 分析

STO 方程是Painleve 可积的[91，94]。考虑下面的截断Painleve 展开形式

将（3.7）代入（3.6），可以得到

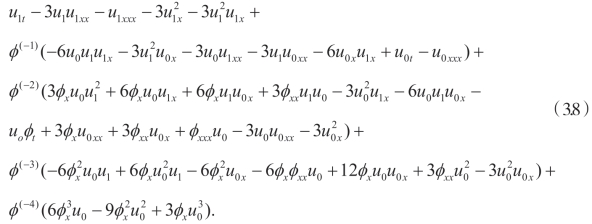
令 ϕ−4的系数等于零，得到

或者

可以得到共振条件 j=1，3 这个方程具有 Painleve 性质[91，94]。此外，从φ0和φ1的系数可以得到下面的引理：

引理 3.1.1 u0=ϕx 是STO 方程的一个对称，而且 u1是方程的一个解。

为了证明这个引理，首先给出对称的定义[57，93]。

定义3.1.1 [57，93] 给定一个非线性发展方程

这里K [u]=K（x，t，ux，uxx，…）。如果 σ（x，t，ux，uxx，…） 是方程（3.11）的一个对称，则 σ满足

这里 K′是Frechet 导数。

引理 3.1.2 σ=σ（x，t，u） 是方程（3.6）的一个对称，当且仅当

这里u 是方程（3.6）的一个解。

从 ϕ0和ϕ1的系数可以得到

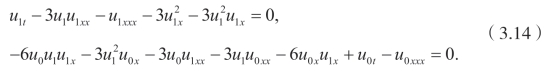
将u0=ϕx和 u1 代入（3.14），可以得到引理（3.1.1）。

需要指出的是，u0=ϕx 是与 Bäcklund 变换（3.7）有关的一个非局域对称。