6.6　李对称分析和行波解

6.6　李对称分析和行波解

现在，利用下面的变换

可以得到

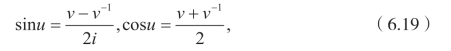
同时有

将（6.48）和（6.49）代入（6.13），可以得到下面的方程

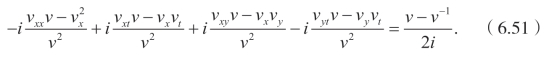
或者

基于李对称方法，假定（6.52）有下面的向量场

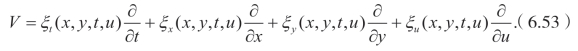
因此可以得到下面的结果

这里F1，F2，F3，F4是x，y，t的任意函数。因此可以得到下面的结果

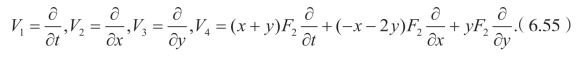
很容易验证（6.52）有两个基本的几何对称

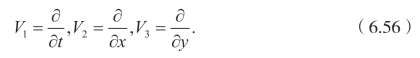
显而易见，（6.52）有行波解。现在，将v（ξ）=f（k1x+k2y−k3t）代入（6.13），可以得到下面的常微分方程

这里A=2k12+2k1k3−2k1k2−2k2k3.

现在假定（6.57）有下面形式的解

这里ϕ满足Riccati 方程

众所周知，Riccati 方程有下面的解

当R<0时有，

(https://www.daowen.com)

当R>0时有，

现在将（6.58）和（6.59）代入（6.57），可以得到

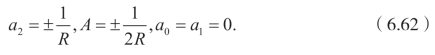
因此，可以得到

当R<0时，有

和

当R>0时，有

和

注记 如果用下面的变换

得到

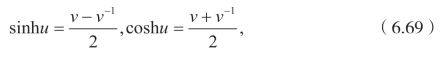
和

可以得到同样的方程，

现在为了得到（2+1）-维sinh-Gordon 方程的解，只需将

换成

即可.