5.1 引言
从守恒律的角度来看，三阶或者更高阶的偏微分方程系统是十分有趣的，因为存在着高阶乘子以及守恒流。众所周知的是KdV 方程和五阶Boussinesq方程。
对于带有弱非线性波（带有弱非线性项）的Burgers-KdV 方程[105]，
这里a，b 和g是常数，u是波的表面。
另一个更为复杂点的系统是演化Jaulent-Miodek 方程组
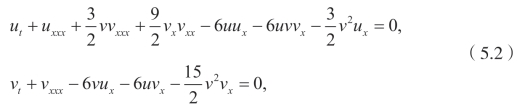
该方程最初是研究非线性演化方程的反散射问题（该反散射问题是和一维Schrödinger 问题相关）时导出[111]。在文献[112]中，作者通过Hamiltonian公式分析了该方程。作者在文献[113]中，研究了该方程的贝克隆变换。作者用He 的迭代方法和Adomian 分解法研究了该方程[114]，无论从数值角度还是分析角度，许多作者都研究了该方程。此外，作者[115]研究了该方程的对称和一些守恒律。然而作者并没有显示地给出对称和乘子的关系。当然，如前所述，有大量的文献 [61，65-72，119-121]去处理非线性偏微分方程的守恒律，在这里不再一一描述。
首先给出一些基本的概念。首先，考虑含有n个自变量x=（x1，x2，…，xn）和 m个因变量u=（u1，u2，…，um）的方程
这里u（1），u（2），…，u（r）分别表示一阶、二阶…，r阶偏导数，也就是 uia=Di（ua），
，…这里关于xi的全导数算子是
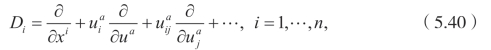
守恒流是指对于Φ=（Φ1，…，Φn）满足
可以发现，对于每一个守恒律都可以从乘子Qµ（x，u，u（1），…）得到，也就是说
对于一些Φi，如果该偏微分方程是变分的，则乘子是变分对称。对于任意给定的偏微分方程，存在一个决定系统去寻找相应的乘子（或者守恒律），之后，可以利用其他公式得到守恒密度。众所周知，对于每一个乘子Qµ，满足伴随方程
这里A
Gµ是Gµ的伴随Frechet 导数。
现在简单介绍一下利用Ibragimov 提出的伴随方程方法[72]的步骤，将会发现该方法（伴随方程、乘子、拉格朗日量）如何适用于高阶方程。这里差别在于，伴随方程的决定方程是通过乘子方法得到的
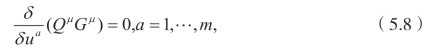
同时，
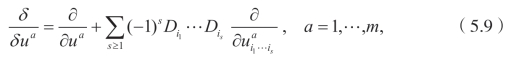
是欧拉拉格朗日算子。对于每一个已知的Qµ，定义函数同时可以发现，类似于前面提到的诺特定理（Noether’s theorem），则可以得到（5.3）的守恒流。也就是说，Φi=Ni L，这里Ni是诺特算子（Noether operator），即
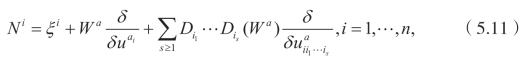
这里，
是（5.3）的对称算子且 Wa=ηa−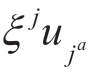
是特征函数。
对于标量方程，记作Qµ=Q，对于方程组，记作（Q，P）为（Q1，Q2），对于含有两个变量（x，t）的方程，记自变量是（x1，x2），同时（Φx，Φt）用（Φ1，Φ2）来代替。