3.3.4　守恒律

这一小节，利用乘子方法去处理守恒律。首先给出一些基本的定义。如前所述，假定方程可以写成守恒律形式 DxTx+DtTt=0。前面已经得到相应的向量场 X1=∂t和X2=∂x。对于特殊的情况n=2，我们得到额外的标量对称X3=x∂x+5t∂t−2u∂u。对于一般的情况，我们仅有乘子Q=1，即守恒向量

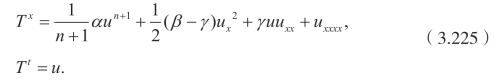
特殊情况，如果β=γ2，可以得到乘子Q=u，于是守恒向量为

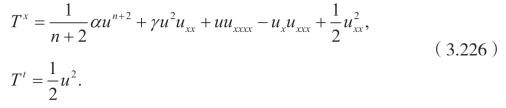
对于n=2，满足下述条件

我们得到一个额外的二阶乘子Q=（（2β−γ）u2+10uxx），和额外的非平凡守恒向量

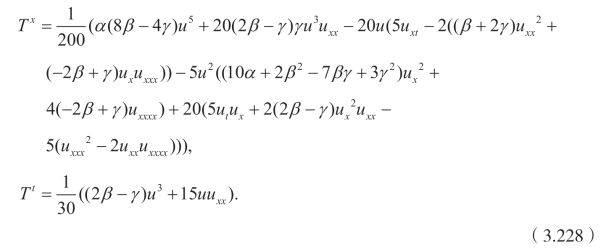
同时注意到，X3作用到 Q满足X3Q=−4Q.对于任意的解u（x，t），如果 u 及其导数项在x→±∞时收敛，则利用得到守恒量。

从前面得到的孤立波解，当δ=1时，可以得到如下守恒量