7.4 本章小结
2026年01月14日
7.4 本章小结
这一章,基于对称研究了分数阶非线性偏微分方程,尤其是通过李对称和守恒律,研究了时间分数阶非线性色散方程。首先给出了该方程的李点对称群,基于对称将方程约化成一个非线性的分数阶常微分方程,此外,给出了该方程的守恒律,得到的结果将会为数值结果、理论分析提供有力的帮助。当然,还有许多问题没有解决,比如在本章,仅仅用经典李点对称群考虑了两个自变量和一个因变量,那么,对于含有更多的变量的方程以及方程组的情况,依然是不清楚的。此外,对于能写成守恒律形式的方程,比如对于本章研究的方程
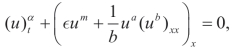
可以写成势系统的形式(https://www.daowen.com)
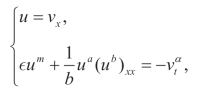
现在问题是,如何求分数阶非线性偏微分方程的非局域对称,或者如何求分数阶非线性偏微分方程的非经典对称,以及如何将整数阶的情况推广到分数阶情况,比如达布变换、贝克隆变换、反散射变换等,都是值得研究的问题。在将来的研究工作中,对于这些问题,将会展开深入的研究。
关于本章以及相关的工作,已经发表在Nonlinear Dynamics、Nonlinear Analysis:Modelling and Control、Laser Physics 等期刊。还有一部分工作已经完成即将投稿。
