4.1.3　守恒律

4.1.3　守恒律

这一小节，利用伴随方程的方法去考虑ZKB 方程（4.1）的守恒律。并考虑其非线性自治性。

4.1.3.1　非线性自治性

对于ZKB 方程（4.1），伴随方程为

拉格朗日函数可以写成对称的形式

在方程（4.29）中，用u替代v后，得不到原方程，因此原方程不是自治的，我们寻找显式的 ϕ（x，u）≠0

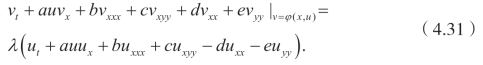
令v=ϕ（t，x，y，u），可以得到

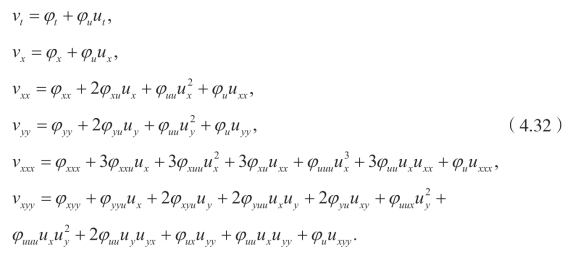
将（4.32）代入（4.31）中可以得到

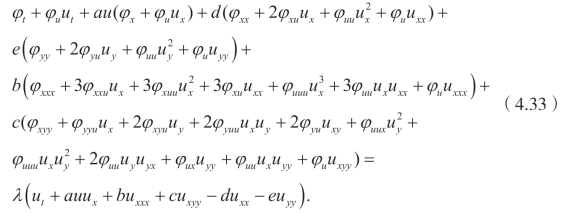
对于ut的系数，可以得到

注意到 u 以及其他独立项的系数，有

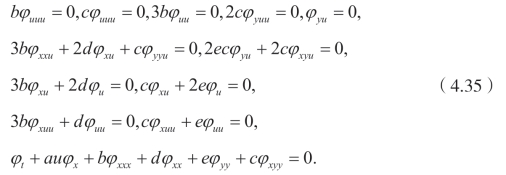
解这些方程，可以得到

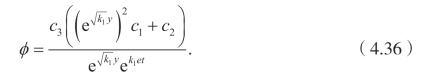
方程（4.35）有下面的特解

这里c1，c2和 c3 是常数。因此，有下面的定理

定理 4.1.1 如果 v=ϕ并且ϕ 由（4.36）或（4.37）确定，则ZKB 方程（4.1）是非线性自治的。

4.1.3.2　守恒律

现在利用伴随方程和对称去构建方程的守恒律，伴随方程是

并且拉格朗日方程是

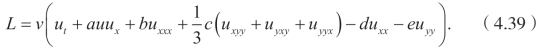
相应的向量场是

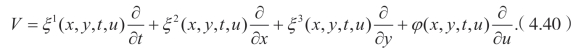(https://www.daowen.com)

算子V 可以导出守恒律

这里 C=（C1，C2，C3） 由下式确定

也就是说

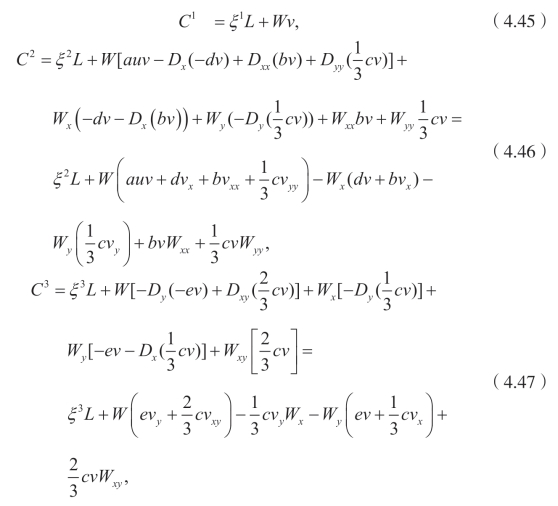
这里

现在来计算守恒律。

情况1.对于算子V=，有

可以得到，

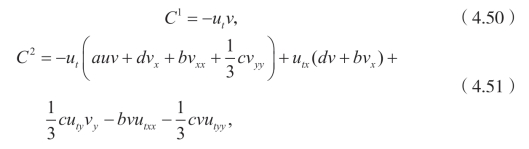
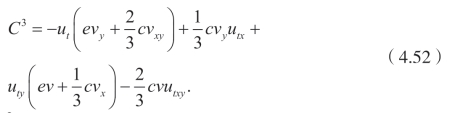
情况2.对于V=，有

类似的可以得到，

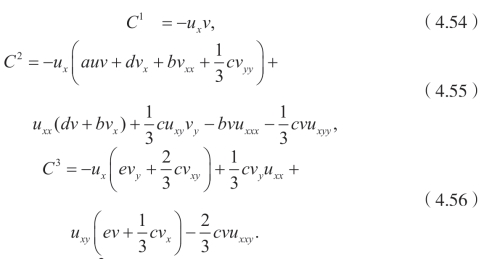
情况3.对于李代数V=，有

可以产生

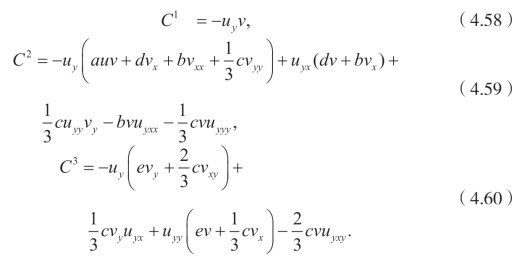
情况4.对于线性组合，有

类似于上面的步骤，可以推出

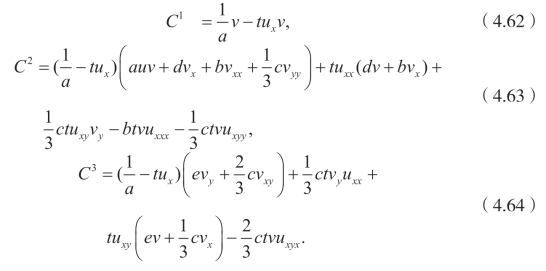
显而易见，守恒向量涉及伴随方程的任意解，所以可以得到无穷守恒律。