3.2.3　非局域对称、线性化和显式解

3.2.3　非局域对称、线性化和显式解

3.2.3.1　势系统的非局域对称

寻找非局域对称是研究非线性演化方程的一项重要工作。因为非局域对称涉及新的变量，所以可以得到新的精确解及非局域守恒律。类似于三阶Burgers方程，可以将四阶Burgers 方程写成下面的势系统

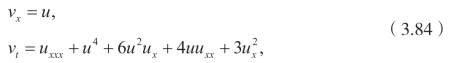
并且将第一个方程代入第二个方程，可以得到下面的势方程

考虑李点对称

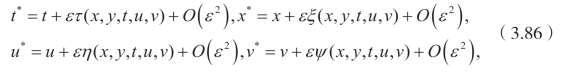
满足下面的方程

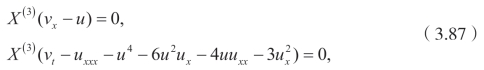
对于任意的（u，v）。此外，无穷小算子是

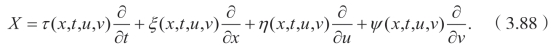
三阶延拓公式为

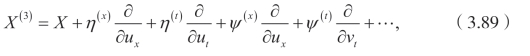
这里

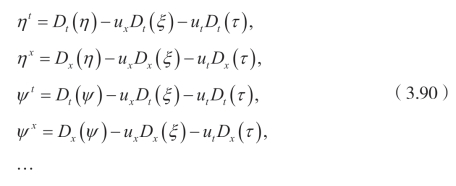
同时，Dx和Dt 依然是全导数算子。

从对称方程，可以得到决定系统，解之得

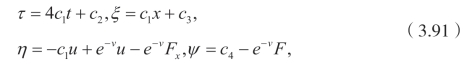
这里 F=F（x，t），且 F满足Ft−Fxxxx=0。因此，得到下面相应的向量场

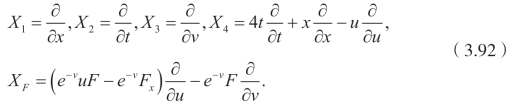
3.2.3.2　通过非局域对称线性化势系统

类似于三阶Burgers 方程，试图从对称的角度将四阶Burgers 方程线性化。首先已经知道

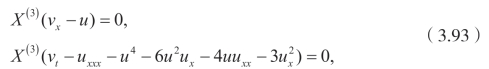
有下面的无穷小算子

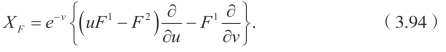
这里F=（F1，F2） 满足下面的线性方程

依然是利用[95，96]中的定理，

并且假定[95，96，98]：

于是有[95，96，98]：

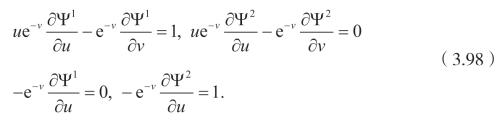
解这几个方程，可以得到

因此，可逆映射µ由下面式子给出

将势系统（3.84）转换成下面的线性系统

并且有

将四阶Burgers 方程转化成下面的四阶线性的偏微分方程

需要指出的是（3.102）正是著名的 Cole-Hopf 变换。

3.2.3.3　四阶Burgers 方程的线性化

为了将四阶Burgers 方程线性化，首先给出四阶线性偏微分方程的对称

再次，考虑经典李群方法，可以得到

相应的向量场为

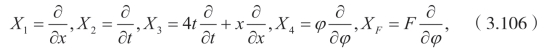
这里，F满足

利用[46] 给出的方法，可以得到

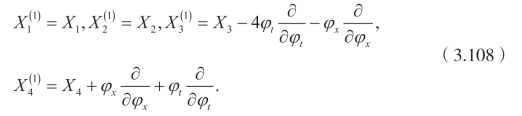
因此，有

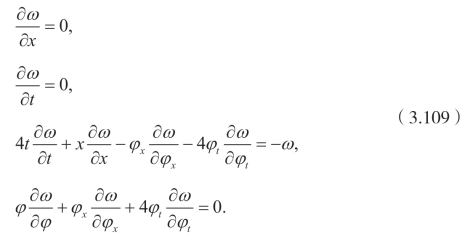
求解上面的系统，也可以得到 Cole-Hopf 变换

再次，从点对称的角度，同样将四阶Burgers 方程转换成四阶线性偏微分方程。

3.2.3.4　通过Cole-Hopf 变换求显式解

从前面的小节可以看到，利用Cole-Hopf 变换，可以将四阶Burgers 方程转换成四阶线性偏微分方程，因此，只要我们得到四阶线性偏微分方程的显式解，再利用Cole-Hopf 变换，可以得到四阶Burgers 方程的精确解。现在考虑四阶线性偏微分方程（3.104）。对于该方程，

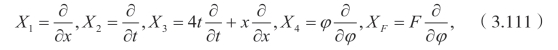
这里

3.2.3.5　一维李代数的优化系统

首先，利用李代数给出优化系统[48]：

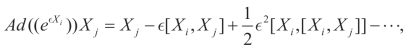
这里∊是实常数。其中[Xi，Xj]是交换李代数，由下面的式子给出

[Xi,Xj]=Xi Xj−Xj Xi.

表1和表2给出了李点对称的交换表和伴随表示。

表1　李代数交换表

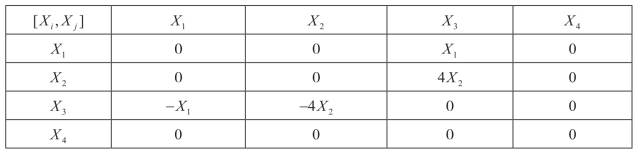
表2　李代数的伴随

(https://www.daowen.com)

可以得到一个一维李代数的优化系统

X3+aV4,a∈R.

X2+bX1+cX4,

这里 b∈−{1，0，1}和c ∈R；如果 b=0，则c∈−{1，0，1}.

X1+dX4,d ∈{−1,0,1}.

X4.

3.2.3.6　显式解

现在，考虑方程的显式解。

（1）对于向量场 X2，可以得到

这里 θ=x。将（3.113）代入（3.104），可以得到

很容易得到该方程的解

利用Cole-Hopf 变换，得到四阶Burgers 方程的显式解为

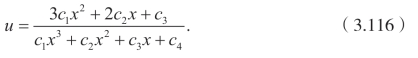
（2）考虑算子X3，有

这里。将（3.117）代入（3.104），有

解这个方程，可以得到

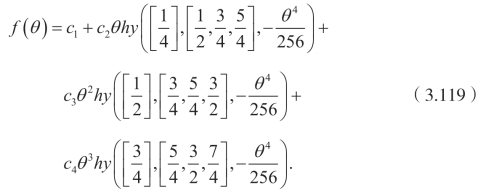
这里hy 是一般的超几何函数。同时，也可以得到

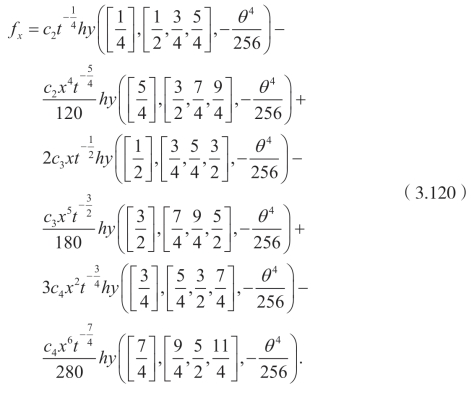
再次利用Cole-Hopf 变换，可以得到四阶Burgers 方程的精确解为

这里 f 和fx分别由（3.119）和（3.120）给出，而。

（3）对于线性组合 λX1+X2，可以得到

这里θ=x−λt。将（3.122）代入（3.104），得到

解这个方程，可以得到下面的情况：

如果λ<0，则

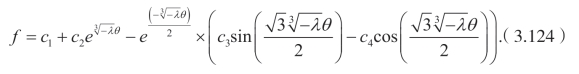
此外，可以得到

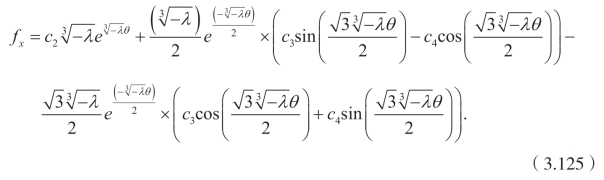
基于Cole-Hopf 变换，可以得到四阶Burgers 方程的显式解为

这里 f 和fx分别由（3.124）和（3.125）给出，θ=x−λt。

当 λ >0时，有

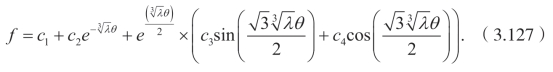
同时可以得到

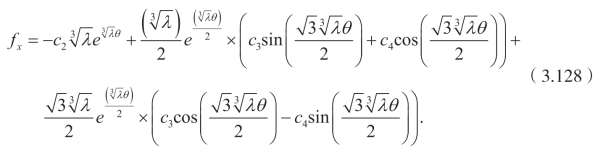
再次利用Cole-Hopf 变换，可以得到

这里 f 和fx分别由（3.127）和（3.128）确定，θ=x−λt。

（4）对于线性组合X2+aX4，可以得到

这里θ=x。将（3.130）代入（3.140），得到

解这个方程，可以得到

如果a<0，则有

其中。同时有

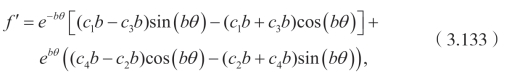
这里。

考虑Cole-Hopf 变换，可以得到四阶Burgers 方程的显式解为

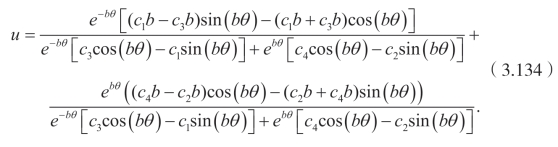
当 a>0时，有

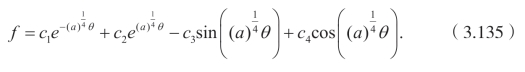
此外还有

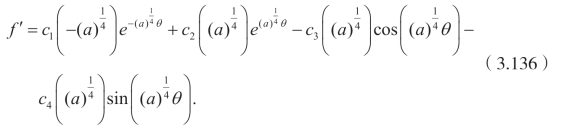
利用Cole-Hopf 变换，可以得到

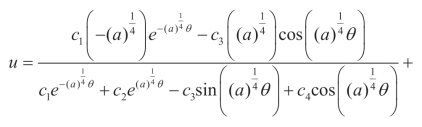
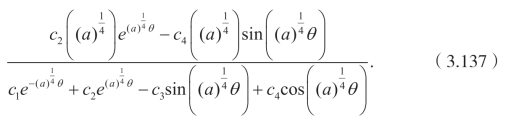
（5）对于向量场X3+aX4，可以得到

这里。将（3.138）代入（3.104），有

解这个方程，可以得到

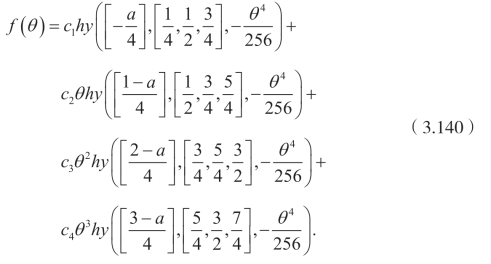
同时可以得到

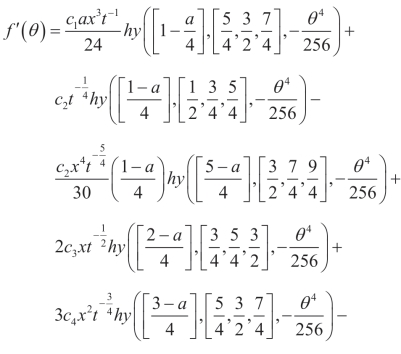
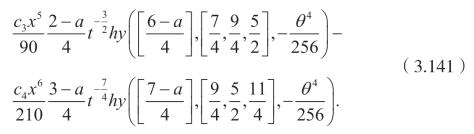
再次利用Cole-Hopf 变换，可以得到四阶Burgers 方程的精确解，这里不再一一列出。