3.1.3 势系统和势方程的李点对称
2026年01月14日
3.1.3 势系统和势方程的李点对称
为了得到更多的非局域对称,利用势系统去分析(3.6)。首先,可以写成下面的势系统的形式

而且可以得到势方程
![]()
李点对称由下面的式子给出
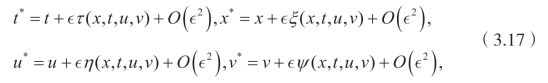
这里∊是群参数,并且
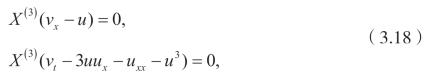
其中(u,v) 满足(3.15),李点对称的无穷小生成元为
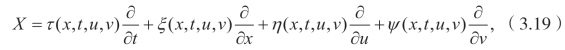
三阶延拓公式为
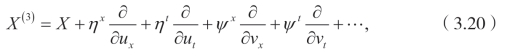
并且
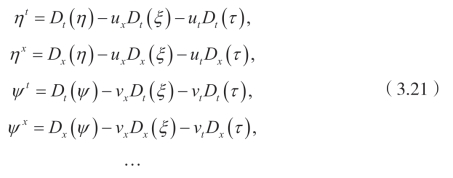
这里,Dx 和Dt 是全导数算子。
定理 3.1.1 势系统(3.15)有下面的李点对称
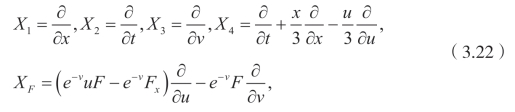 (https://www.daowen.com)
(https://www.daowen.com)
并且
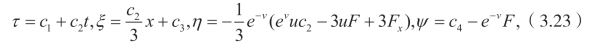
这里 F=F(x,t),并且 F 满足 Ft−Fxxx=0。因此,STO 方程拥有相应的势对称。
证明:利用李点对称,可以得到下面的超定方程组
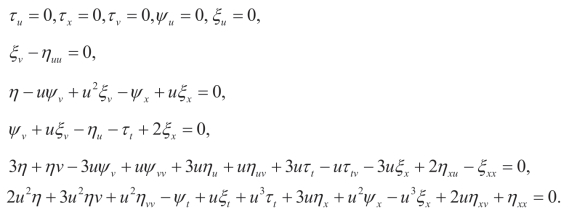
解这些方程,可以得到(3.22)和(3.23)。
定理 3.1.2 势方程(3.16)拥有下面的李点对称
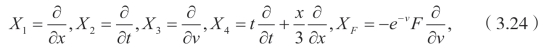
和
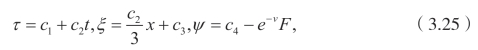
这里F=F(x,t),且F 满足同样的方程Ft−Fxxx=0。
证明:类似于上面的步骤,可以得到
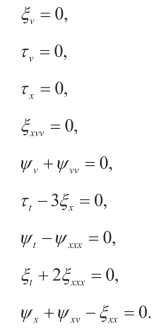
解这些方程,可以得到(3.24)和(3.25)。
注记:
1.在上面的向量场中,向量场 XF 是势对称(非局域对称),它们从经典李点对称是得不到的。
2.如果存在守恒律的形式,利用守恒律去构建非局域对称不是唯一的方法。此外,并不是所有的守恒形式,或者说势系统都能导出非局域对称。
