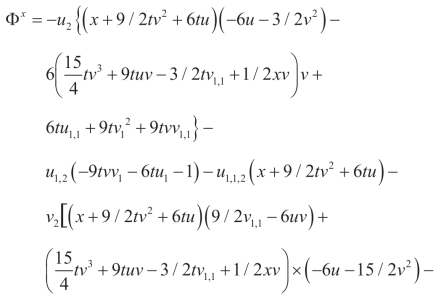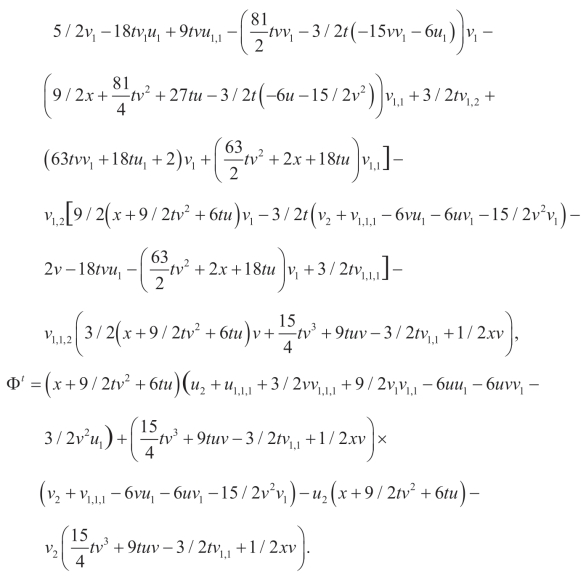5.2　应用

5.2　应用

例1.首先考虑Burgers-KdV 方程（5.1），其李点对称算子是

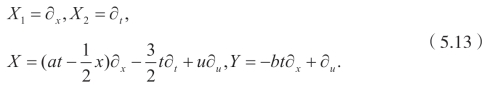
利用（5.8），二阶乘子Qi可以推出非平凡守恒律如下

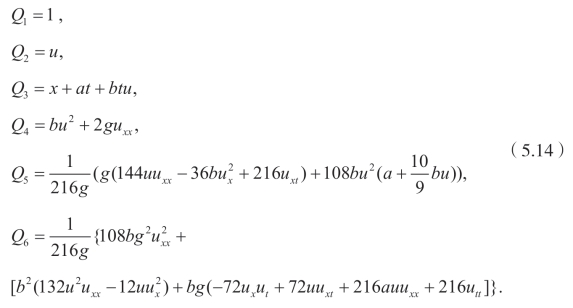
需要注意的是每一个Qi都满足伴随方程

例如，对于乘子Q2=u，代入方程（5.1）中可以得到

有趣的是对于高阶乘子，比如Q4，经过化简，方程（5.16）左边变成

其他乘子可以类似验证，从而发现乘子也满足伴随方程。因此，可以发现，对于高阶乘子所对应的守恒律，也可以通过伴随方程方法得到。

在本书分析中，会利用乘子Q1到Q5；Q6计算繁琐但是过程一样，所以不再详细列出。基于乘子和对称，相应的守恒向量场列出如下。

在下文中，如无特别说明，下标1和2 分别是指关于x和t的偏导数。

（i）Q3，X2:

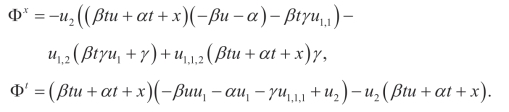
（ii）Q3，X1：

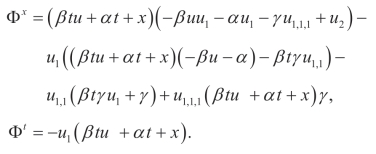
（iii）Q2，Y:

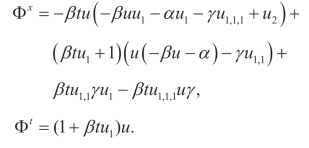
（iv）Q4，Y:

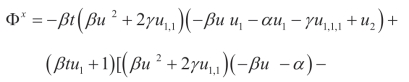
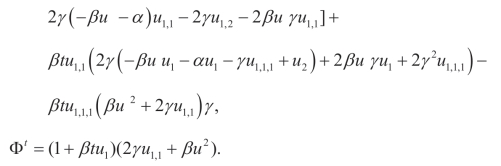
（v）Q1，X:

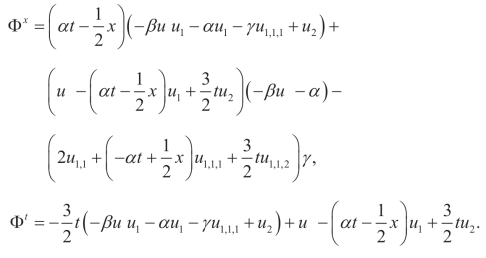
（vi）Q2，X:

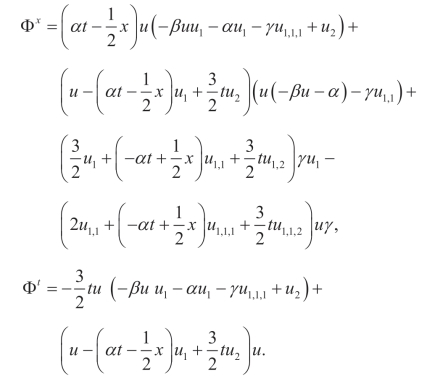
（vii）Q4，X:

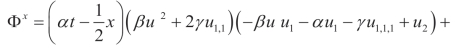
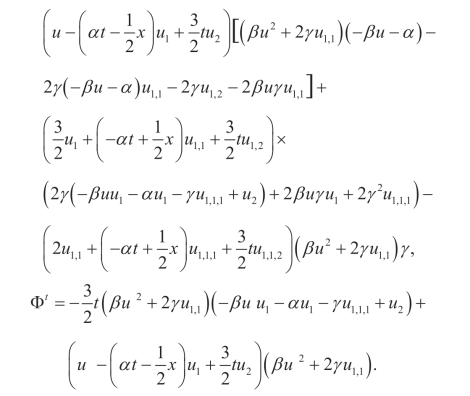
（viii）Q5，Y:

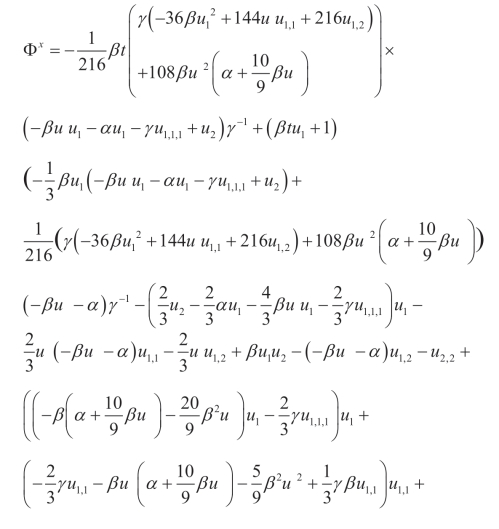
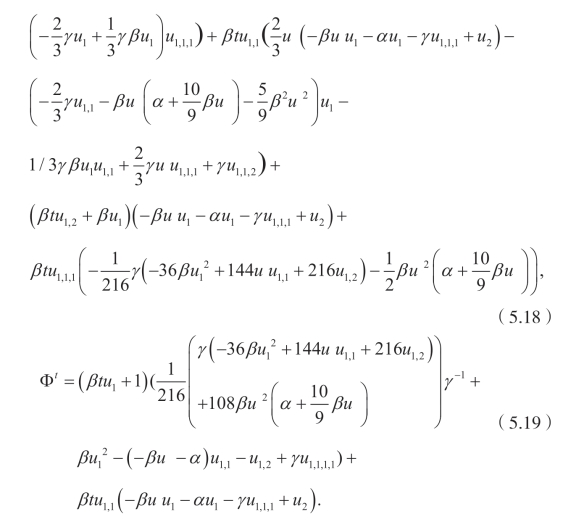(https://www.daowen.com)

（ix）Q5，X1:

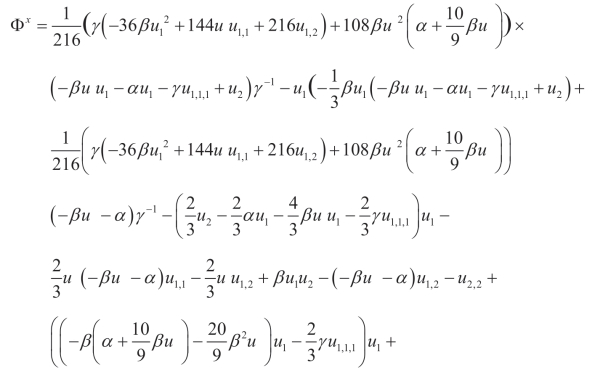
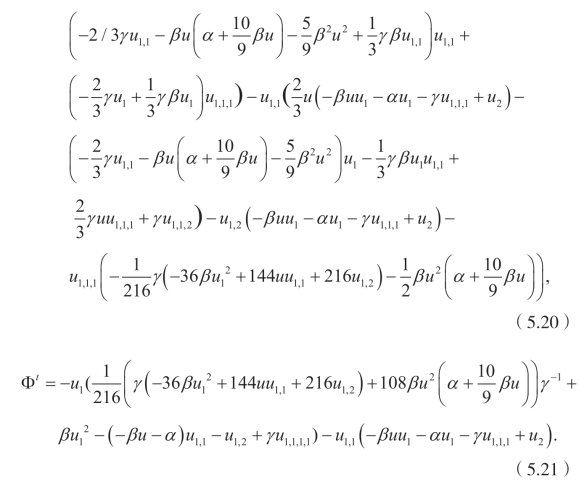
（x）Q5，X2:

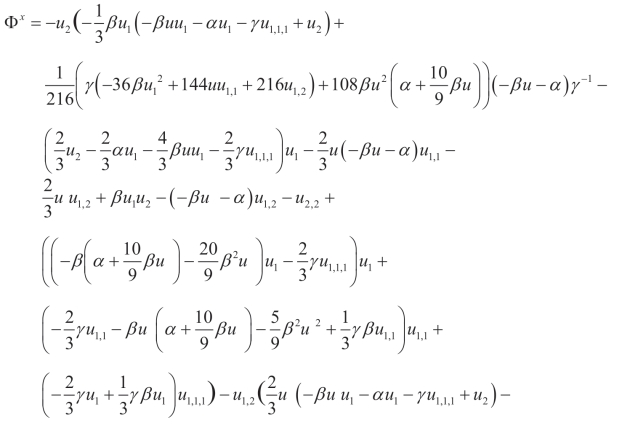
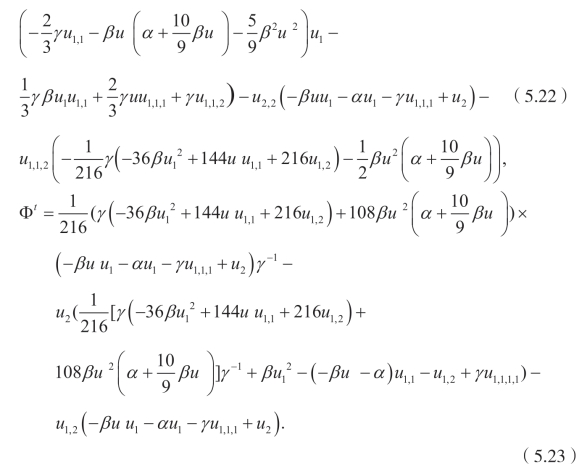
（xi）Q5，X:

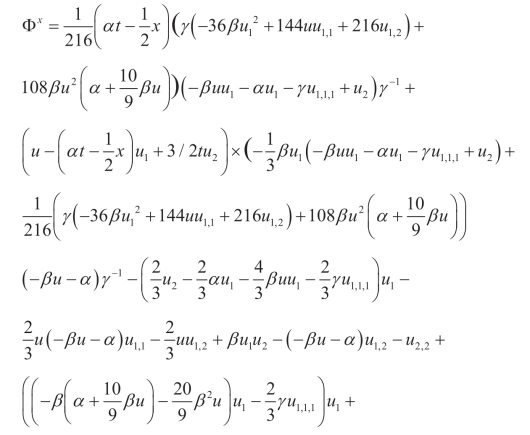
例2.第二个例子是演化的Jaulent-Miodek 方程组（5.2）。相应的对称

和二阶乘子分别是（Qi，Pi）

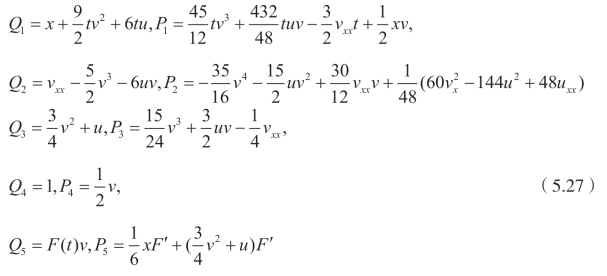
再次，利用前面的步骤可以得到

（i）(Q1,P1):

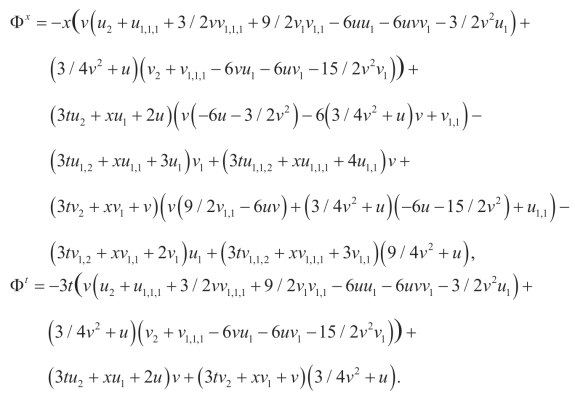
（ii）(Q2,P2):

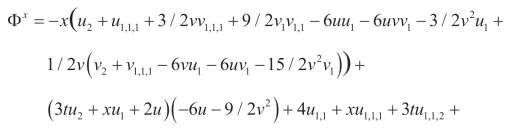
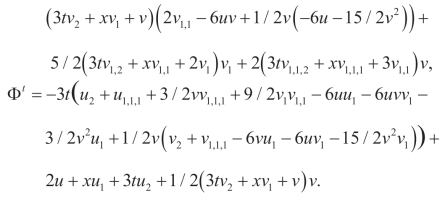
（iii）(Q3,P3):

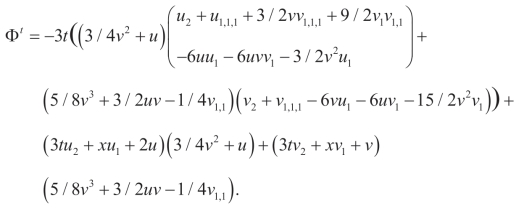
（iv）(Q4,P4):

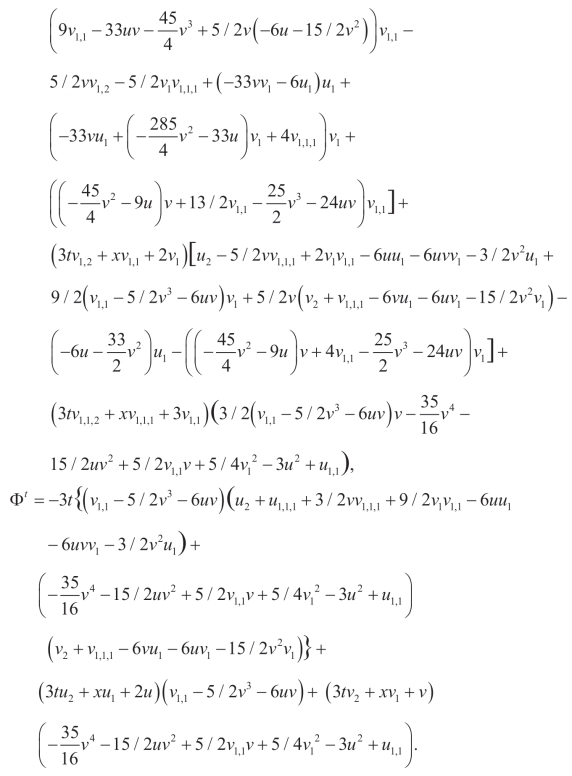
（v）(Q5,P5):

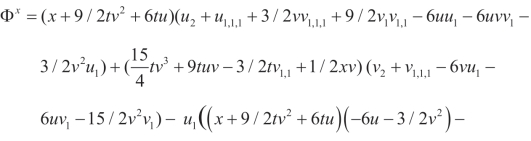
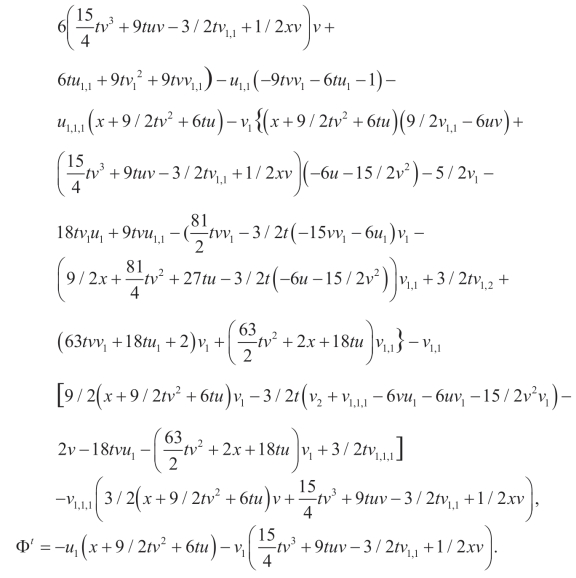
利用（Q5，P5），可以得到另外的非平凡守恒流

（vi）