3.2 EGs 的构成和基本概念
3.2.1 EGs 的构成
皮尔斯指号学的分类,把我们引向对述位、命题和论证的关注。EGs 作为一个逻辑,自然要关注对指号解释的这一分类。我们在前面已经从指号的可视性角度,说明EGs 产生的一个动因。从EGs 产生的时间序列来看,皮尔斯在19世纪的末叶构建了逻辑代数,在构建逻辑代数的过程中,他就开始对逻辑的图表式表述感兴趣。代数逻辑中的合取式A∧B,这种合取式的交换性质,皮尔斯以一对语句实例的形式,设想到可以用图表来表示它们。
设有语句1:天打雷。设有语句2:天下雨。这两个语句构成的合取语句“天打雷并且天下雨”,我们就可以用以下图表来揭示合取的交换律,四个方框内的语句虽然位置不同,但它们都是等价的语句。[25]
皮尔斯的这个构想,可以看作EGs 的一个雏形,其中粗线条框定的平面,在后来建立的EGs 中,被看作是断定平面。细线条框定的命题,可以看作是给命题一个图标。在皮尔斯的晚年,他花费很大的心力来构建有关逻辑推理的图表系统,他构建的成熟的逻辑系统就是EGs。EGs 由相关的三个系统组成,一个是表达命题逻辑的Alpha 图表,一个是表达一阶谓词逻辑的Beta 图表,第三个则是表达模态逻辑或者高阶逻辑的Gamma 图表。EGs 不仅意图处理由陈述句所表达的思维,还想处理非陈述的语句,例如疑问句和祈使句所表达的思维。以下,我们先给出EGs 相关的一些基本概念,以便讨论EGs 中的Alpha 图表和Beta 图表。皮尔斯的模态构想是本章之后的讨论重点,将专列一章,另行解释和分析Gamma 图表。
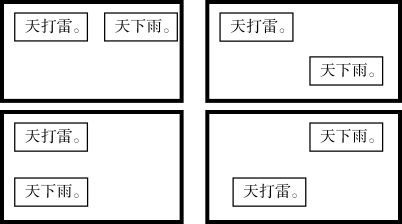
图表5 合取语句的等价图表表述
3.2.2 EGs 的Alpha 图表
Alpha 图表有三个初始词项,一个初始词项是命题符号,一个初始词项是割线(cut),第三个初始词项是并列(juxtaposition)。
任意大写字母A,B,C…,表示命题的符号,有时候我们也用带下标的大写字母表示命题符号,例如A1,A2…。
围绕命题符号的封闭线条(可以是圆圈,也可以是方块,由你约定。本文约定用圆圈表示割线),它表示对命题的否定,这类线条我们称之为“割线”。
以下图表6 中的命题公式,其中的(2)、(3)、(4)、(5)分图中的命题之间的关系,都可以看作是并列关系,类似于命题逻辑中的合取。
Alpha 图表中基本的图表符号是断定平面,断定平面SA(Sheet of Assertion)类似于我们在图表5 中的粗线方框。该方框中没有被割线圈定的命题符号,就是被我们肯定的符号。有割线封闭的符号,就是被我们否定的符号。如果断定平面为虚空,它就类似于命题逻辑中的重言式,常常用符号┳(verum)表示。
我们可以列举几个图形来说明这些基本概念。
设A 和B 是命题,则以下图形分别表示命题逻辑中的以下断定公式。
┳=(1),├A=(2),├A∧B=(3),
├¬(A∧B)=(4),├¬ A∧¬ B=(5),
├¬(¬ A∧¬ B)=(6)=├A∨B。
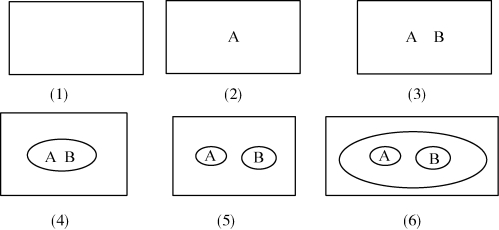
图表6 Alpha 图表中的命题公式
由这两个初始词项和断定平面图形,我们就可以构成一个Alpha 图表逻辑系统。设这个图表系统为G0,则显然这个G0包括:
①虚空的断定平面。
②命题符号。
③并列闭包:如果A1,A2…An 分别在G0 中,那么这n 个指号的并列也在G0 中,n 个指号的并列称之为并列闭包。
④割线闭包:如果A 在G0 中,则割线所选择的A 也在G0中,割线所选择的A 称之为割线闭包。
使用这样一个Alpha 图表系统,我们几乎可以刻画命题逻辑中的所有东西。如同以上描述所示,并非、合取和析取表达式已经得到了解释。但还没有揭示,在Alpha 图表系统中如何表达条件句,也就是经典命题逻辑中的实质蕴涵。自然,对一个蕴涵式:“如果A,那么B”,如果我们要用Alpha 图表来描述它,一定是把它放在一个断定平面上。皮尔斯使用了一个术语scroll,似乎相当于中文的卷轴。什么是卷轴?皮尔斯给出一个说明:两条封闭的线条,一个线条在内,一个线条在外,就构成一个卷轴。[26]
如图表7 中的(1)所示。
如果我们把命题A 置于外圈,把命题B 置于内圈,由此我们就获得了图表7 中的(2),这就是我们刚才所说的条件句:如果A,那么B。
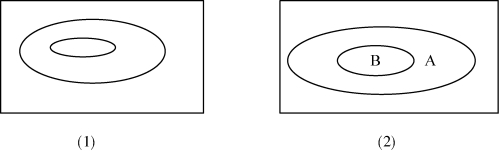
图表7 皮尔斯的卷轴概念图表
把图表7 中的图表(2)看作是条件句,直观上似乎很合适。A 和B 不是合取,因为不在一个圈中,但依据我们在Alpha图表系统中的基本词项,它是可以用合取与否定来解释的。图(2)中的圆圈是割线,代表否定。A 所在圈既是对A 的否定,也是对B 否定的否定,而A 和否定B 处在并列位置,自然是合取。因此图(2)可以解释为:并非是这种情形:A 真并且B假。这个图有没有另外的读法?我们先读B 的两次否定,再读A的一次否定,由此得A 假并且B 真。皮尔斯看到了这种读法,所以他给出了EGs 的视读要求,这个要求他用一个怪癖的词项endoporeutic来表示,中文翻译应该为:向内进行的视读法。
存在图表的解释是endoporeutic,那是向内进行的过程;以便一个巢箱吸纳着从外到其中心的意义,如同海绵吸收水一样。[27]
如果按照这种向内进行的视读方法,条件句不是初始词项,而是依据否定和合取定义而来。但从皮尔斯文献中来看,他似乎更希望有一个直接的条件句读法,不用借助否定与合取来间接说明蕴涵。卷轴概念我们还会在EGs 的另两个图表中涉及,对Alpha 图表系统的描述我们暂且到此,以下,我们在Alpha 图表系统基础上,描述皮尔斯EGs 中的Beta 图表。
3.2.3 Beta 图表
Beta 图表系统类似于带等词的一阶逻辑,除了我们在Alpha图表系统中的初始词项之外,我们再加上等同线LI(Lines of Identities)就构成了Beta 图表系统。这个等同线指称一个对象的存在,可以有许多分支,这些分支称作连字符(Ligatures)。所以,Beta 图表系统中的等同线就可能是点(dots),也可能是连续线(contiguous line),还可能是等号(identity)。如果Beta 图表和一阶逻辑比较,这个等同线类似于一阶逻辑的谓词、存在量词和等词。
为了更清楚地表述Beta 图表系统,还需要依据皮尔斯的原著引进一些相关术语。第一个是“节点”(spot),我们在前面已经有过说明,皮尔斯称之为“述位”(rhema),它很类似于我们讲过的带空位的命题形式。
例如:是好的,这是一元的述位命题形式。再例如:
喜欢,这是二元的述位命题形式。自然,还有n 元的述位命题形式。在这些命题形式之中,等待填入的位置称之为空位(hook),在上述例子中,一个短下横线就是一个空位。与空位对应的是一阶逻辑的谓词,它表达命题中某个对象的性质。由此,Beta 图表系统中的一个节点就是一个谓词。设这个谓词为P,则我们可以用有限个空位,即n 个空位作为谓词的标记,这就形成了一元到n 元的谓词。这就是说,有一个空位的是一元谓词,有n 个空位的就是n 元谓词。这些表达对象数量的标记,放在谓词的上标位置,如果对象数为1,则可以省略。
我们仍然用具体的图表,来说明这个等同线的解释,并在解释的过程中继续刻画Beta 图表系统中的一些其他术语。
假定P(x)=x 是好的,Q(x)=X 是丑的;R(x)=x是有用的,则我们可以在以下图表8 中,用等同线来表述这几个命题形式。
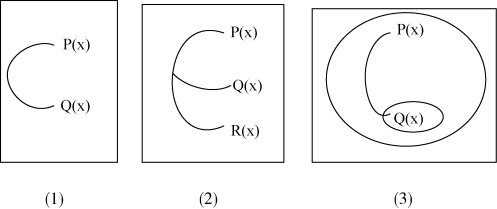
图表8 等同线的图例
图表8 中的三个子图表达的全是一元谓词,图(1)中弧线就是等同线,指称了有对象存在。等同线显然有两个端点,这两个端点上的某些对象既具有好的性质,也具有丑的性质。图(2)中有三个端点,两条等同线,这表示有某些东西具有好、丑和有用的性质。图(3)除了有等同线,还有否定性质的割线,也是两个端点,这个图表明:凡是好东西都不丑。
那么如何表达二元谓词R(x,y)?这需要借助泽曼在研究皮尔斯EGs 时引进的一个术语:松散端点(loose end)。[28]如果一条等同线的两端没有附加的谓词在其后,则这条线的两端就是松散端点。因此,每一条等同线在不附加任何指号的条件下,它的两个端点就是松散端点。例如图9 中的等同线的两个末端,没有附带任何符号,这些等同线的每一个末端就是松散端点。

图表9 松散端点图表
由这个松散端点的概念,我们就可以表述二元的或者三元的,以至n 元的谓词。皮尔斯构建EGs 的首要动机,就是意图用图表来表述关系。
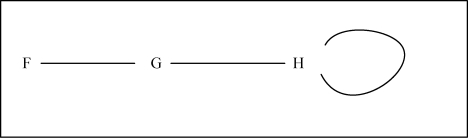
设F 是一元谓词,G 是二元谓词,H 是三元谓词,我们就可以使用以下图表10 来表述这三种谓词,谓词所涉及的个体就是图中每一个松散端点。
图表10 一元、二元和三元谓词的Beta 图表
很明显,在图表10 中,左端的F 只有一个松散端点,中间的G 有两个松散端点,而右端的H 有三个松散端点。松散端点相当于我们语言中的一个类型(type),当把一个具体的个体填入的时候,这些个体就是语言中的一个例(token)。
Beta 图表作为一阶逻辑另一种表述方式,其中的全称量词和存在量词该如何理解呢?现在就可以进行说明了。皮尔斯原创EGs 图表中的两个量词,依据皮尔斯的原文是很难理解的,好在有现代学者对他原创想法进行诠释。皮尔斯对EGs 图表中量词的讨论,其主要的观点罗伯特(Roberts,Don)在其1973年的论文中作过比较容易理解的描述。罗伯特给出了四个图表,然后对这些图表予以解释,正是这个解释道出了Beta 图表系统全称量词和存在量词的表述方式。[29]
 (https://www.daowen.com)
(https://www.daowen.com)
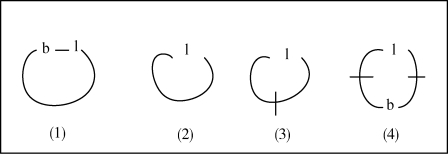
图表11 Beta 图表系统的全称量词和存在量词
图表11 试图解释四个谓词语句,其中的等同线末端可以表达个体,或者规定一下论域,作为人的个体。如果等同线是松散端点,我们就可以将其读作“某些人”。如果等同线中间有填入的交叉线条杠[见图(3)、图(4),这些线条杠不应理解成等同线],这样的表达式就是全称的表达式,对应于一阶逻辑的全称量词:所有人或者每一个人。图(1)中的B 表示施者(benefactor),一个语句的主体,l 表示爱者(lover),所以图(1)翻译为语句就是:某些人是他所爱的人的施者。图(2)施者与爱者同一,该图的语句就是:某些人是自己的爱者。图(3)是全称语句:所有人都是自己的爱者。图(4)也是全称语句:每一个人或者是自己的爱者或者是自己的施者。
那个不应该属于等同线的线条杠(bar)按照诗茵(Sun-Joo Shin)的说法,不属于图表的表达式,而是属于代数逻辑的表达式,[30]这留给以后再来讨论。
由以上Beta 图表系统的简要解释,我们可以获得以下一些类似于一阶谓词逻辑公式的EGs 图表的表达式,图表12 给出了这类表达式,并对Beta 图表系统的两种量词给予进一步的解释。
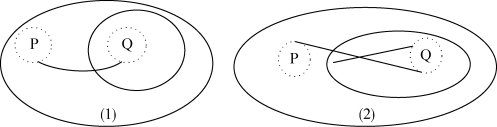
设P、Q 为两个节点,相当于谓词,我们略去断定平面,构建以下Beta 图表表达式。
图表12 类似于一阶谓词逻辑公式表达式的Beta 图表表达式
图表12 中的(1)类似于一阶逻辑的谓词公式∀x(P(x)→Q(x));
图表12 中的(2)类似于一阶逻辑的谓词公式∀x∃y(P(x)→Q(x,y))。
图(1)依据前面卷轴的定义,P 所在命题和Q 所在命题是蕴涵式P(x)→Q(x)。图(1)中有两条虚线圆圈等同线,一条等同线用连字符和P 的割线相连,另一条和Q 的割线相连,两条线的交点在Q 的内层割线上,表示两个谓词的个体等同。这断定了在断定平面的论域内任意个体x,如果x 有性质P,那么x 就有性质Q。
图(2)也是一个条件公式,但在等同线的连字符上有区别。一条在终端相连,这表示了全称量词的含义;另一条则在Q的割线内终止,这对P 而言,表示存在量词的含义。所以,我们可以把这个图(2)看作是
∀x∃y(P(x)→Q(x,y))。
依据以上简略可能并不准确的描述,我们可以构成一个Beta图表逻辑系统。设这个图表系统为Gβ,则显然以下术语包括在Gβ 中:
①虚空的断定平面。
②等同线符号。
③并列闭包:如果P,R,…S(n 个谓词符号)分别在Gβ中,那么这n 个谓词符号图表的并列也在Gβ 中,n 个谓词符号的并列图表称之为并列闭包。
④谓词闭包:如果P 在Gβ 中,则带有n 元谓词符号的图,那些符号在P 中写在n 个松散端点的交点上,它称之为谓词闭包,也在Gβ 中。
⑤割线闭包:如果P 在Gβ 中,则在P 的任意子图表中不用穿越谓词符号挑选出的图表,它称之为割线闭包,也在Gβ 中。
⑥分支闭包:如果P 在Gβ 中,则在P 中的一个等同线的若干分支的图表,它称之为分支闭包,也在Gβ 中。
3.2.4 Alpha 图表和Beta 图表简略小结
对EGs 这两个图表的描述,可能会产生这样一个疑惑,Alpha图表和Beta 图表仅仅对应于一阶逻辑的语形方面的考虑,其中有关演算的部分似乎完全没有涉及,语义方面的设计则一直都没有讨论。而皮尔斯出于图表的可视性特征所构建的这两种图表逻辑系统,在体现可视性方面也缺乏必要的分析。进一步,在经典实用主义哲学背景下,作为弄清楚概念语词意义的一种方法的图表逻辑,它何以能够明确概念?也是我们需要回答的问题。所有这些,我们将在给出皮尔斯Gama 系统,他所构想的模态系统之后一起来讨论。
【注释】
[1]参见http:∥en.wikipedia.org。
[2]美国实用主义经过一百余年的发展,有许多不同的实用主义流派,最基本的流派是经典的实用主义,分析的实用主义,新实用主义,概念论的实用主义,新经典的实用主义,等等。为行文方便,本文所指的实用主义,如不特别说明,都是经典意义上的实用主义。即由实用主义的三杰(类似于古希腊三杰苏格拉底、柏拉图和亚里士多德):皮尔斯、詹姆斯和杜威的基本观念所代表的实用主义,一般称之为经典实用主义。
[3]威廉·詹姆斯著,陈羽纶、孙瑞禾译:《实用主义》,商务印书馆1997年版,第26—27页。
[4]参见科尼利斯·瓦尔著,郝长犀译:《皮尔斯》,中华书局2003年版,第79—80页。
[5]参见http:/ /www.oao.com.cn/ShowArticle.asp?ArticleID=21。
[6]苏珊·哈克主,陈波、尚新建副主编:《意义真理与行动——实用主义经典文选》,东方出版社2007年版,第144页。
[7]路易斯·梅南德著:《美国观念的故事》,江苏人民出版社2006年版,序言第2页(该书中的哲学俱乐部,按我的理解,应该翻译为形而上学俱乐部)。
[8]苏珊·哈克,陈波、尚新建副主编:《意义真理与行动——实用主义经典文选》,东方出版社2007年版,第5页。
[9]参见涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第41—43页。
[10]参见涂纪亮编《皮尔斯文选》,社会科学文献出版社2006年版,第22—40页。
[11]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第45页。
[12]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第45页。
[13]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第55页。
[14]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第102页。
[15]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第276页。
[16]涂纪亮主编:《莫里斯文选》,社会科学文献出版社2009年版,第183页。
[17]Ahti-Veikko Pietarinen,Signs of Logic,Springer 2006,P22.
[18]参见保罗·科布利、莉莎·詹茨著:《视读符号学》,安徽文艺出版社2007年版,第28页。
[19]参见涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第168—172页。
[20]Ahti-Veikko Pietarinen,Signs of Logic,Springer 2006,P29.
[21]参见涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第277—278页。
[22]涂纪亮编:《皮尔斯文选》,社会科学文献出版社2006年版,第287页。
[23]Ahti-Veikko Pietarinen,Signs of Logic,Springer 2006,P115。
[24]Ahti-Veikko Pietarinen,Signs of Logic,Springer 2006,P104。
[25]Edited by Cheryl Misak,The Cambridge Companion to Peirce,Cambridge University Press 2004,P306—307.
[26]Sun-Joo Shin,The Iconic Logic of Peirce's Graphs,MIT Press,Cambridge,2002,P72.
[27]Roberts,Don(1973),The Existential Graphs of Charles S.Peirce.The Hague:Mouton,P39.
[28]Zeman,Jay(1968),The Graphical Logic of C.S.Peirce Ph.D.Diss.University of Chicago,P72.
[29]Roberts,Don(1973),The Existential Graphs of Charles S.Peirce.The Hague:Mouton,P19.
[30]Sun-Joo Shin,The Iconic Logic of Peirce's Graphs,MIT Press,Cambridge,2002,P50.
