1.4 用符号逻辑方法建立的命题演算
1.4.1 对命题符号的两种解释
如我们在经典逻辑历史发展的脉络中所描述的，布尔构建了逻辑代数，这可以看作是符号逻辑的开端。布尔的逻辑体现以下三个基本观念：
（1）“选择”运算观念和“选择符号”观念；
（2）对这些符号进行运算的规则，可表达为“思维法则”的观念；
（3）同等遵循的观念，这些运算法则在数字0 和数字1 的代数中是同样成立的，自然需要同等的遵循。[7]
布尔的逻辑代数可以用来处理词项，它最先就是用来处理三段论中的词项的，所以最先的符号逻辑是关于词项的符号逻辑。但这一逻辑也考虑到命题，它用数字1 和0 分别代表命题的真和假。这就产生一个问题，当我们说一个命题是真或者是假的时候，我们所讨论的对象是命题本身还是和命题相关的什么东西？
这个区别应该是很重要的。当我们说一个命题p 或者真，或者假的时候，这和我们说某个命题p 为真，某个命题q 为假，这两者之间是有区别的。前者是假定任意一个命题形式p 的真值，这种假定真值的命题使用，实际上面对的不是命题，而是命题函数。而当我们说某个命题具体的真值的时候，这个时候，我们面对的才是命题。但布尔那个时候还没有看到这种区别，布尔是在两个方面都有过运用，但更多的是用在命题函数方面。最先看到这种区别的应该是皮尔斯和施罗德，他们在命题和命题函数之间进行了区分，布尔代数不需要做出这种区分，但如果增加一个规则给这个逻辑，则这个逻辑处理命题是合适的，处理命题函数却是不合适的。这个规则可以表述为：“如果p假，那么p 真。”因为皮尔斯和施罗德做出了这一区分：
他们并入这个附加原则的结果就发展了命题演算，而通过并入下述观念“p 有时真”，“p 总是真”，“p 有时假”，“p 总是假”，他们又发展了命题函数的演算。符号化这些概念的结果，发展那些适合于两类演算法则的结果，是命题函数演算获得意义深远的扩张，这种扩张超越于依据布尔代数可以符号化的东西。[8]
因此，了解现代逻辑早期的理论，布尔施罗德代数是不能忽略的。我们将从这个代数系统开始，再给出二值代数系统，然后引申出实质蕴涵基础上的命题演算。
1.4.2 布尔-施罗德代数
布尔最先创建布尔代数，然后由施罗德、皮尔斯等人完善修改。布尔代数较完整地体现在施罗德所著的《逻辑代数》一书中，C.I.刘易斯称这种代数为布尔-施罗德代数，它实际上是一个关于类，或者是关于词项的演算。布尔-施罗德代数的基本构件，全都用抽象意义的符号来表示，已经具有今天命题逻辑的几乎所有要素，这些要素分别是：5 个初始符号，3 个相关定义，6 个公设。和欧式几何的公理化系统一样，没有推演规则，我们按现今通用符号陈述如下。
（1）初始符号
①字母a、b、c……表示任意词项，或者任意类。
②∩表示逻辑乘（交）。
符号a∩b 表示，a 和b 共有的成员，它既属于a，也属于b，常被读作a 并且b。
③┑表示逻辑否定。
┑a 表示不属于a 的那些成员类别，读作并非a。
④0 表示空类。
如果一个对象没有包含任何成员，我们就称这个类为空类，用0 表示。
⑤=表示相等。
类a 和类b 有完全相同的成员，我们可以表示为a=b。
（2）相关定义
由以上初始概念，我们引入下述定义。
①定义：1=¬ 0，和空类0 对应的类是全类，用1 表示。
②定义：a∪b=¬（¬ a∩¬ b），和逻辑乘对应的是逻辑加，用∪表示，a∪b 表示或者是a 类，或者是b 类所构成的类，常被读做a 或者b。
③定义：a⊂b 等价于a∩b=a。
⊂是包含于关系，皮尔斯创立了这种关系，a⊂b 表示，a 的成员一定在b 之中，但b 的成员却不一定在a 之中，常被读做a包含于b。
（3）公设
①a∩a=a。
这个公设可以称作同类相乘的吸收率。
②a∩b=b∩a。
这个公设可以称作逻辑乘的交换律。
③a∩(b∩c)=(a∩b)∩c。
这个公设可以称作逻辑乘的结合律。
④a∩0=0。
这个公设可以称作逻辑乘的归零律。
⑤如果a∩¬ b=0，那么a⊂b。
这个公设可以称作逻辑乘和包含于关系的条件律。
⑥如果a⊂b，并且a⊂¬ b，那么a=0。
这个公设可以称作包含于关系的归零律。
（4）基于初始概念、定义和公设推演出的几个布尔定理
①如果a=b，那么a∩c=b∩c，并且c∩a=c∩b
证明：
根据=的定义，a=b 表示a 和b 有同样的成员，c 和c 有同样的成员，所以a∩c=b∩c。再根据交换律自然c∩a=c∩b。
证毕。
②a=b 等价于a⊂b 并且b⊂a。
证明：
如果a=b，根据公设①：a∩b=a∩a=a；b⊂a=b∩b=b；
根据定义③：a⊂b 等价于a∩b=a，所以a∩b=a∩a=a 就是a⊂b。
同理b⊂a=b∩b=b 就是b⊂a。
所以a=b 等价于a⊂b 并且b⊂a。
证毕。
③0⊂a。
证明：
根据交换律，0∩a=a∩0；
公设④：a∩0=0，所以0∩a=0；
根据定义③：a⊂b 等价于a∩b=a，所以0⊂a。
证毕。
④a⊂1。
证明：
根据定义②：a∪b=¬（¬ a∩¬ b），我们有a∪¬ a=¬（¬ a∩¬ ¬ a）=¬（¬ a∩a）；
根据公设⑥：如果a⊂b，并且a⊂¬ b，那么a=0，
则有（¬ a∩a）⊂a，（¬ a∩a）⊂¬ a，所以（¬ a∩a）=0。
根据定义①：a∪¬ a=¬ 0=1，所以a⊂1。
证毕。
1.4.3 二值代数
显然，对于布尔-施罗德代数系统的各个构件，在我们把有关词项的理解转化为有关命题的理解，并且在6 个公设基础上再增加一些有关真值的公设的时候，这个类的系统就变成了命题的系统，C.I.刘易斯称之为二值代数。它作为一个数学系统，由布尔-施罗德代数系统的所有法则构成。[9]对照布尔-施罗德代数系统（以下凡称布尔代数的地方，如无特别说明，都是指布尔-施罗德代数），以下给出的是这个二值代数系统的基本构件。
（1）初始符号
①p，q，r……代表任意命题。（这对应布尔代数的任意类a，b，c 等）
②¬ p 表示p 的矛盾命题，它表示对p 的否定。（这对应布尔代数的否定）
③p∨q 表示析取命题“或者p，或者q”，也就是在p 和q这两个命题中至少有一个命题是真的。（这对应布尔代数a∪b）
④0 或者⊥表示假。（这对应布尔代数的空类0）
⑤≡表示等值，p≡q，表示p 和q 两个命题等值。也就是，或者p 并且q 都是真的，或者p 并且q 都是假的。（这对应布尔代数的=）
（2）相关定义
①定义：1=¬⊥=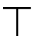
=¬ 0=真。（这对应布尔代数的全类1）
②定义：p∧q=¬（¬ p∨¬ q）。（这对应布尔代数的a∪b=¬（¬ a∩¬ b））
③定义：p→q=¬（p∧¬ q），p→q 表示“如果p，那么q”，也就是p 蕴涵q。（（这对应布尔代数a⊂b。布尔代数公设6：如果a⊂b，并且a⊂¬ b，那么a=0，使用蕴涵符号就变成以下的命题逻辑表达式：如果（p→q）并且（p→¬ q），那么¬ p。这实际上就是以下二值代数的公设⑥）
（3）二值代数公设
①p∧p≡p。
这个公设对应布尔代数同类相交的吸收律a∩a≡a。
②p∧q≡q∧p。
这个公设对应布尔代数交运算的交换律a∩b=b∩a。
③p∧(q∧r)≡(p∧q)∧r。
这个公设对应布尔代数交运算的结合律a∩（b∩c）=（a∩b）∩c。
④p∧0≡0。
这个公设对应布尔代数交运算的归零律a∩0=0。
⑤如果p∧¬ q≡0，那么p→q。
这个公设对应布尔代数逻辑乘和包含于关系的条件律“如果a∩¬ b=0，那么a⊂b”。它实际上就是¬（p∧¬ q）≡p→q的另一种表达方式。
⑥如果p→q，并且p→¬ q，那么p≡0。
这个公设对应布尔代数包含于关系的归零律，如果a⊂b，并且a⊂¬ b，那么a=0，它实际上就是著名的归谬律，如果一个命题推出矛盾，则这个命题是假命题。
二值代数不同于布尔代数的地方，表现在公设的设置方面，除了上述布尔代数的公设，二值代数还附加了公设⑦。
⑦(p≡0)≡¬ p。
这个公设告诉我们，如果一个命题符号p 被指定为假，则这个为假的符号p 就等值于¬ p。由于这个公设的引入，二值代数可以导出布尔代数中没有的定理。C.I.刘易斯正是依据这个看似直观的公设⑦，得到一些他认为有些别扭的命题，这些命题后来就被称作为实质蕴涵怪论。
布尔代数中的定理，在二值代数中仍然是有效的。但如果利用二值代数的附加公设⑦，则推出的定理全都不是布尔代数中的定理，它们仅属于二值代数系统，在这个二值系统中，C.I.刘易斯开始讨论他所关注的实质蕴涵怪论。
1.4.4 实质蕴涵怪论
二值代数系统的专有定理几乎全都和蕴涵相关，这个用符号“→”表示的蕴涵，和我们日常语言中的蕴涵含义有一些差异。我们从以下导出的定理中可以发现，这些定理似乎有点脱离我们对蕴涵的直观。之所以出现这种情形，是因为这种蕴涵所表达的关系是外延性质的，这种蕴涵就是实质蕴涵。在二值代数中，我们可以导出不属于布尔代数的那些实质蕴涵表达式定理。
(1)p→(q→p)
这个定理表达的是：如果p 为真，则这个真命题p 为任何命题q 所蕴涵。这个定理的证明可以使用二值代数的附加法则和消除法则。
因为有二值代数附加公设⑦：（p≡0）≡¬ p，就有p≡（p=1），所以有（q→p）=1，根据p→1，再有p→（q→p）。这个定义表明，一个真命题为任何命题所蕴涵。
(2)¬ p→(p→q)
因为有（p=0）≡¬ p，根据0→p，所以有p→q=1，再根据p→1，我们就有¬ p→（p→q）。这个定理告诉我们，一个假命题可以蕴涵任何命题。
(3)(p∧q)→(p→q)
(4)(p∧q)→(q→p)
根据p→（q→p），可得以上定理，也可以得到以下的定理。
(5)(¬ p∧¬ q)→(p→q)
(6)(¬ p∧¬ q)→(q→p)
(7)(¬ p∧q)→(p→q)
(8)¬(p→q)→p
(9)¬(p→q)→¬ q
(10)¬(p→q)→(p→¬ q)
(11)¬(p→q)→(¬ p→q)
(12)¬(p→q)→(¬ p→¬ q)
(13)¬(p→q)→(q→p)
以上列出的13 个实质蕴涵的定理，都来自于以下4 个有关真值的直观上可得到的法则，它们分别是：
R1.0→p,
这就是假命题蕴涵着任何命题。
R2.p→1,
这就是真命题被任何命题所蕴涵。
R3.(p≡0)≡¬ p,
这就是二值代数的附加公设⑦，一个命题为假，意蕴着其否定命题¬ p 为真。这应该看作是命题逻辑的初始假定，任何一个命题仅只具有两个值0 或者1。
R4.p≡(p≡1)。[10]
这显然是二值代数的附加公设⑦的另一种对偶式的理解，一个命题以肯定的形式出现，就表示它已经为我们所断定，这就自然是真的。这样，在二值代数系统中出现的所有命题形式，以否定出现的命题形式那就表明那整个负命题为真，以肯定形式出现的，就表示这个符号本身是真的。这实际上就是命题演算中的断定关系，通常用├表示。
显然，这些法则把我们对命题的演算，变成一种基于二值的演算，我们所处理的命题符号p、q、r 等仅仅只有1 和0 两个值，从而完全撇开了对命题意义的理解。这种对命题符号外延式的理解是布尔代数处理类演算的自然结果，空类对应于假，全类对应于真。在布尔代数中，类的性质为构成类的对象来决定，而这个类的对象正好就是词项的外延。把布尔的类演算变换成处理命题演算的二值代数，命题的意义抽象为真和假，命题意义本身似乎就不见踪影，暂时被我们搁置一旁。这样一种处理命题的方式，实际上是把真假看作是命题的外延，是一种外延演算的代数式系统。
在外延传统的二值代数中，当我们用符号p、q、r 表示任意命题的时候，这些命题如果没有否定符号置于前，我们把这些命题符号看作是真的；如果有否定符号置于前，我们把这些命题看作是假的。依据这样一个设定，我们就获得一些与实质蕴涵相关的定理或者法则。这些法则体现在上一节1.4.2 列出的公式中，从（1）到（13）表述的就是这类定理。这些有关蕴涵的法则从直观的意义或者常识的意义上看，让人们觉得有些不顺，它们并没有对应于蕴涵的通常意义。因此，C.I.刘易斯将它们称作“蕴涵怪论”。在C.I.刘易斯那本《心灵和世界秩序》的著作中，他用揶揄的语气来评论这样一种蕴涵的法则，他提到以上给出的定理（2）和定理（3）。
例如，罗素先生把他的整个结构建立在一种蕴涵关系上（指实质蕴涵），其结果是，如果从一张报纸上剪下20个句子，把它们放进一顶小帽子里，然后从中随机抽出两个来，那么其中的一个必定蕴涵另一个，而且，两者相互蕴涵的机会是均等的。《数学原理》的整个结构就是建立在这样一个如此远离日常推理模式的基础之上的。[11]
虽然从二值代数中可以导出这些实质蕴涵的定理，但从逻辑斯蒂方法的角度看，使用C.I.刘易斯的论述，二值代数还不是基础，我们可以借助于对二值代数的分析还原到基本的命题演算，这个演算的典型例子就是罗素与怀特海在《数学原理》中给出的命题演算。实际上，C.I.刘易斯对实质蕴涵的质疑，本来就是对罗素和怀特海《数学原理》一书中有关蕴涵的质疑，这个蕴涵就是实质蕴涵。从二值代数中出现的实质蕴涵，是C.I.刘易斯后来的概括。这个概括表明，并不是二值代数包含于罗素和怀特海的命题演算之中，反倒是，它作为命题演算的一个扩充，自然要包含命题演算中已经存在的实质蕴涵怪论。
1.4.5 《数学原理》中的命题演算
我们已经知道，命题是具有真值的语句表达式，而真值有真（1）和假（0）两个值，这样的命题系统自然就是二值代数系统。而当我们把作为语句表达式的命题用函数的方式来理解的时候，我们就有了“命题函数”的概念。
C.I.刘易斯是这样来定义命题函数的。
命题函数是含有一个变元或者若干个变元的表达式，当我们对每一个变元赋给一个值的时候，这个命题函数就成为一个命题。[12]
命题函数中表达谓项的符号，用希腊字母φ、ψ 表示。表达主项的符号，用小写字母x、y、z 表示。一个命题函数可以表示为φ（x），如果函数是二元的，可以表示为φ（x，y），等等。我们显然并不知道这样的函数形式是否真或者是否假，因为主项x 随着我们给它赋予不同的对象值，它会有不同的真值。就此而言，命题形式φ（x）具有清晰的函数性质，它就是一个命题函数，谓项是它的不变量，主项是它的变量。假定我们用a、b、c 等来表示主项被赋给的不同值，例如用a 来赋给φ（x）中的x，则我们就有命题φ（a）。
显然，C.I.刘易斯在这里给出的定义，其中的变元不是命题变元，而是词项的变元。这里的值也不是赋给命题的真值，而是赋给词项变元的对象值，这种分析方式是代数式的。当要用逻辑斯蒂的方法建立他的严格蕴涵系统的时候，这就需要不同于代数方法的《数学原理》中的初始观念了。按照罗素和怀特海关于初始观念的构想，他们先给出基本命题观念，进而给出基本命题函数观念。在不同于代数方法的初始观念之下，二值代数中的命题形式p、q、r，可以仅在基本命题的形式下予以指派，由此而构成最为基本的逻辑演算系统。[13]
如果我们将表达命题的符号p、q、r 看作是原子命题，不考虑这些命题形式本身的构成，它们就是不再予以分解的符号形式。由此而构成的命题演算，变成了与词项（或者类别）无关的演算系统。这产生了一个未曾预料的结果，原先我们看作是逻辑基础的布尔代数，在布尔代数基础上的二值代数，它们的基础性质好像是颠倒过来了。用逻辑斯蒂方法建立的现代逻辑，其中的命题演算竟成为现代逻辑的基底，成为现代逻辑最为基础的东西。
这种逻辑斯蒂方法建立起来的逻辑系统，它的第一分支即基始的分支，应该是罗素和怀特海《数学原理》中给出的命题演算。这正如《数学原理》所言：
在类的理论中，我们借助于属于命题理论的原则从另外的命题推演出一个命题，而在命题的理论中，我们在任何地方都不需要类的理论。因此，在一个演绎系统中，命题理论必然地在先于类理论。[14]
这种命题演算理论，对所有由命题陈述的那些法则，不用提及词项，也不用提及词项之间的关系。对于进入词项间关系而形成的那些命题，我们也仅把它们看作是进行了结构分析的命题。由此，我们在二值代数中所做的工作就包含着命题演算的工作。这样，历史上出现的一些逻辑系统，不是以时间序列来决定它内容是否扩充，而是以命题演算为基础的一个扩充序列。首先是命题演算，在此基础上，我们可以建立命题函数的演算。而从命题函数的演算，我们又可以再导出类演算和关系的演算。[15]这里提及的所有这些演算，因为处理的都是符号所指谓的外延，这样的演算也可以称作是外延的演算。布尔创建的布尔代数，以及建立在实质蕴涵基础上，在罗素和怀特海《数学原理》一书中的命题演算，都是外延演算的典型系统。
前面，我们按时间顺序，先给出基于类演算的二值代数，它是将布尔-施罗德代数应用于命题的结果。由此，而形成一种类似于命题演算的系统。现在，我们又已经知道C.I.刘易斯有关命题函数的解释，那么，我们换一个思路来理解符号逻辑的这些最早的进展。如果我们把布尔-施罗德代数解释为命题演算，这种命题演算实际上不是关于命题的，而是关于命题函数的。当代数解释为集合或者类，它们完全不是命题函数，只有代数表达的是命题，这样的命题解释就成为命题函数。
可以把这样的命题函数分为两大类，一类是一元命题函数，另一类统统归之为多元函数。好在C.I.刘易斯对命题函数的关注重点在一元函数，正是在这个基础上C.I.刘易斯扩展出他的严格蕴涵系统。为了简洁，我们略去C.I.刘易斯关于多元函数以及关系逻辑的讨论，单论他的一元命题函数。
全部一元命题函数的表达式，都可以归之于我们在上面已经给出的符号φ（x），x 表达的是任意个体对象，φ 则看作为个体对象所具有的性质。这个思想很重要，由一元到多元，又衍生出更多重要的观念，非常自然地包括了很多数学推理的本质。一元命题函数形式的发现，对它的应用既成为现代逻辑的基础，也使得古典逻辑从此发扬光大起来。
因为x 是一类个体中的任意一个，如果我们以符号a、b、c来表示x 各个不同的指派，通常的说法是给以不同的值，符号φ（a）、φ（b），等等，就从命题函数变成了有所断定的命题。而我们对x 的理解，既可以是它的全部，这产生回应古典逻辑的全称量词∀，也可以是它的一部分，这产生回应古典逻辑的存在量词∃。一个有点趣味的结果是：这些量词可以置于命题函数之前，由此所产生的表达式竟然已经不是命题函数，而是可断定其值的命题。但是，我们的命题演算不需要涉及量词，所以关于这两个量词的论述我们也就到此为止。
命题逻辑之所以是命题逻辑，那就是，基本命题函数中的变元被我们给定值之后，换一种表达式，被我们断定之后，这个基本命题我们可以表示为一个无须再分解的命题形式p，p 可称作基本命题或者原子基本命题。这个基本命题的界定，正是《数学原理》命题演算系统（以下简称为PC）的主要初始观念。
我们照录罗素和怀特海《数学原理》中关于基本命题和基本命题函数的论述，先给出他们关于基本命题的说明。
（1）基本命题。使用基本命题这个名称，我们意指它不涉及任何变元，或者我们换一个说法，这类命题不涉及“所有”、“有些”以及等价地表达这些语词意义的量词。一个命题，例如：“这是红的”，其中的“这”是在感觉上给以人的某种东西，这样的命题就是基本的。任何由否定、析取或者合取逻辑符号来联结给定基本命题所构成的合成命题也是基本的。
显然，如果用符号来表达这些基本命题，小写英文字母p、q、r、s 等表示的就是基本命题，这些独立小写字母符号表达的命题，通常称为原子基本命题。这些字母的联结词组合也是基本命题，这通常称为复合基本命题。因为量词的限定被我们搁置一边，原子基本命题本身只能是不加分解的。
我们再照录罗素和怀特海关于基本命题函数的论述。
（2）基本命题函数。使用基本命题函数这个名称，我们意指一个这样的表达式，它含有未经判定的某个构件（这是一个变元），或者几个构件（这是几个变元）；并且使得，当未经判定的某个构件或者几个构件被判定的时候，即，当有值指派给单一的变元或者多个变元时，所论及的这个表达式的值所形成的结果就是一个基本命题。所以，如果p 是未判定的基本命题，并非p 就是基本命题函数。[16]
从二值代数的描述中就可以感觉到，命题演算包含在这个代数之中。在二值代数中增加公设⑦的结果，我们才获得一系列有关实质蕴涵怪论的定理。所以，我们可以把二值代数中的一部分内容整体地剥离，命题演算就从中浮现出来。它的基本构件仍然是初始符号、相关定义、相关公设。然而，罗素和怀特海的高明之处在于，如同它对“基本命题”和“基本命题函数”的界定所表明的，它关注这一形式系统所处理的命题符号是不是合法的符号。同时，《数学原理》对形式系统的构建，还特别关注到推理所使用的规则。这样，在有基本命题和基本命题函数这些初始观念的同时，这一命题演算增加了形式系统的第4 个构件：推理规则。而在初始符号、相关定义的选择上，秉承最少的初始符号来导出其他的导出符号原则，这就使得初始符号和相关定义也产生相应的变化。
其中的初始符号部分，对真值的指派用“断定”符号表示，《数学原理》把断定分成了两种断定，即命题断定和命题函数断定，它实际上是元语言的符号├，也就不再作为初始符号出现。遵循初始符号尽量少的原则，在二值代数中的等值符号可以从其他初始符号导出，等值符号就转移到定义部分。二值代数以∧为初始符号，而命题演算PC 以∨为初始符号。
其中的定义部分，因为断定符号可以不作为初始符号，对真假的互为定义也就不再必要，它们实际上是元语言的东西。
命题演算PC 的公理部分，《数学原理》称之为初始命题。初始命题在很大程度上是个任意选择的结果，但选择的原则还是有的，那就是一个逻辑系统的完备性需要和一致性需要。原先在二值代数中用等值公式表示的公理，涵盖了比命题演算PC更大的范围，等值公理全都使用蕴涵式公理表示，PC 采用皮亚诺的说法把公理用“初始命题Pp”来表示。稍有不同的是，PC中的初始命题①和命题⑦不用符号方式表达，但其他的均采用符号表达方式，因为初始符号是∨，初始命题大都用∨来表达。读者可以对照《符号逻辑》和《数学原理》两书，来加深对这个演算系统PC 的理解。
（1）初始符号
①p，q，r……代表任意命题。
②否定符号¬，¬ p 表示p 的否定命题。
③析取符号∨，p∨q 表示析取命题“或者p，或者q”。
④辅助符号“（”和“）”。
（2）相关定义
①定义：p∧q=¬（¬ p∨¬ q）。
②定义：p→q=¬ p∨q。
③定义：p≡q=（p→q）∧（q→p）。
（3）公理
①被一个为真的前提所蕴涵的任何命题也是真的。
②├：p∨p→p
③├：q→p∨q
④├：p∨q→q∨p
⑤├：p∨(q ∨r)→q∨(p ∨r)
⑥├：(q→r)→((p∨q)→(p∨r))
⑦实变元识别公理。
《数学原理》中给出的公理⑦，称之为实变元识别公理，它不是用一个公式表示的，而是由一段描述来展示公理的基本内容。仅当所涉及命题函数中有实变元识别需要时，才会用到这个公理。
以下，按照《数学原理》的相关陈述，我们给出PC 的推理规则。
（4）推理规则[17]
①分离规则。
命题p 被断定，并且命题“p 蕴涵q”被断定，则命题q 被断定。
②等值替换规则。
如果一个命题p 出现在任意命题f（p）中，并且，如果p≡q，则我们有f（p）≡f（q）。
③一致性替换规则。
任意命题符号p，可以用任意其他命题符号q、r、s 等替换，只要这种替换在该符号出现的每一个地方都一致性地进行。
C.I.刘易斯的严格蕴涵系统，就是在质疑这一演算系统PC的基础上构建的。