2.4　一致性和可能性概念之下的严格蕴涵系统

2.4　一致性和可能性概念之下的严格蕴涵系统

以上讨论的严格蕴涵系统LSIS，C.I.刘易斯是把严格蕴涵p⇒q定义为¬◇（p∧¬ q）。按照C.I.刘易斯的思路，虽然我们有一致性的初始观念，把可能性看作是一致性，但如果我们引进一个一致性符号○，单用这个一致性符号来说明严格蕴涵，这就能够为我们理解模态算子◇提供更为清晰的路径。有了○这样的新符号，我们既可以说明◇，也可以说明⇒。用一致性概念来刻画严格蕴涵系统，为我们提供了一个逻辑研究的新视角。而由于这样的新视角，C.I.刘易斯所构建的严格蕴涵系统，就成为最初的模态逻辑系统。

2.4.1　一致性、可能性和必然性

在LSIS 中，我们有定义①至③，在此基础上我们引入一致性符号○，由其构成的命题p○q，我们给出以下的定义④。

④Def p○q=¬(p⇒¬ q)

这个定义意味着，命题p 和q 是一致的，等值于“p 严格蕴涵并非q，这是假的”。依据一致性的这个定义，以及我们对严格蕴涵的模态◇定义，这可以转换为：

p○q=¬(p⇒¬ q)=¬ ¬◇(p∧q)=◇(p∧q)

如果我们所要考察的是单一命题p 本身和其本身之间的一致性，同样的转换过程所获得的结果是：

这表明，我们对一致性的理解完全可以等同于对◇的理解，所以，一致性就是可能性。那么，C.I.刘易斯为什么要把一致性和可能性作为两个不同的符号引入他的LSIS 呢？这是因为，一致性表达的是命题之间的关系，而可能性只是表达命题真值程度的模态函数而已。而一旦把可能看作是表达命题真值程度的函数，我们就可以依据这种对可能的理解，自然地导出相关于可能的“不可能”观念、“可能不”观念和“必然”观念，这些表达模态的基本观念在实质蕴涵的基础上似乎更容易刻画严格蕴涵系统。使用一致性概念构成的这种严格蕴涵系统等价于LSIS，我们将其缩写为LCCS。因为其公式的基点在模态函数◇p，它就很自然地导引出一系列模态词之间的关系。

很明显，依据p○p=◇p，以下命题结果自然可以得到。

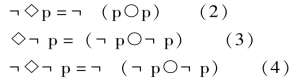
上述命题（2）、（3）、（4）分别表示了：p 是不可能的，p是可能不的，p 是不可能不的。而命题（4）的这种含义恰恰就是必然的含义，亚里士多德的模态三段论给出的这个公式，直观上也是极容易接受的等价式。一个命题“p 是‘不可能不’的”，它表达的就是“p 是‘必然’ 的”含义。由◇定义的这个必然模态，就把实质蕴涵和严格蕴涵之间的关系非常清晰地表达出来。

严格蕴涵和实质蕴涵之间的这种关系，实际上也可以看作是LCCS 和PC 之间的关系。当我们把LCCS 中的严格蕴涵表达式转换为使用模态□或者◇来表达的时候，C.I.刘易斯1932年在《符号逻辑》中的严格蕴涵系统可以看作是模态命题系统的S1。但当我们讨论C.I.刘易斯的“严格蕴涵系统”的时候则要小心，C.I.刘易斯1918年在《符号逻辑概论》中给出的“严格蕴涵系统”不是S1，而是S3。

2.4.2　严格蕴涵和模态逻辑的S1-S5

按照修斯（G E Hughes）和克瑞斯韦尔（M J Cresswell）的说法。

第一个对于严格蕴涵系统的全面处理（或者说真正的、称得上完全的模态逻辑系统）出现在1932年由C.I.刘易斯和兰福德合写的《符号逻辑》一书中。在那里，可能性作为初始模态被采用，并且两个严格蕴涵的公理系统（分别称之为S1 和S2）得到相当详细的发展。在该书的附录中，其他的系统也被概括出来：其中的一个是C.I.刘易斯概论中的系统（S3）；另外的两个，含有贝克（Becker）的归约公设，它们分别称之为S4 和S5。^[22]

从系统构建的时间顺序来看，情形略有不同。最早的严格蕴涵系统出现在C.I.刘易斯1918年的《符号逻辑概论》一书中，其初始符号、公理设置都和1932年的《符号逻辑》有区别。例如，在1918年的系统中，初始符号就特设了一个“不可能”的否定符号，这在1932年的LSIS 中没有了。公理的设置原先有p⇒¬ ¬ p，其后，发现其中一个错误，C.I.刘易斯遂于1920年予以了更正。这个系统包含8 个公设，C.I.刘易斯在《符号逻辑》附录中告诉我们，这个1918年的严格蕴涵系统就是后来在附录中给出的S3。先有了这个S3，然后我们才有S1和S2。

C.I.刘易斯早年关于严格蕴涵的研究，有时候采用“严格蕴涵”，有时候采用“析取”，有时候采用“逻辑不可能性”作为建构逻辑系统的初始符号。但1932年的《符号逻辑》一书，由C.I.刘易斯撰写的几章（包括附录），“可能性”和“一致性”概念统一地作为初始符号应用于他所建构的严格蕴涵系统之中，这在该书首先形成了系统1 和系统2，用英文缩写自然可以分别表示为S1 和S2。

依照在这一章发展起来的方法，我们已经证明有两个互为关联但又有区别的系统。系统1，它由业已给出的定义和本章第一节所给出的公设演绎地构成，并且这个系统含有所有前面T 原则形式下已经证明的定理。系统2，它由业已给出的定义和本章第一节所给出的公设演绎地构成，另加上公设19.01（译者注：该公设是◇（p∧q）⇒◇p），不仅这个系统含有所有这一部分的定理，如同这里所印出的，而且，这个系统还含有用没有T 原则的相应定理来取代的任意T 原则定理。^[23]

依据C.I.刘易斯的这个陈述，S1 就是我们在本章2.4.1 节给出的严格蕴涵系统LCCS，C.I.刘易斯在LCCS 中给出7 个公设，但麦金西（C C Mckinsey，1908—1953）1934年在他论述这个系统的一篇论文中指出：S1 中的公设5 可以从其他几个公设中导出，是不具独立性的公设，所以，这个S1 的公设应该是6 个。^[24]

在《符号逻辑概论》中，C.I.刘易斯构造的不是S1，他先有“严格蕴涵系统”，然后把包含在该系统中的一个子系统称作是“普通推理演算”。

这个普通推理演算包含在严格蕴涵系统之中。它由所有那些严格蕴涵命题构成，这些命题并不涉及实质蕴涵关系p→q（或者实质逻辑并p∧q）。但是，在严格蕴涵中我们有¬◇p 的地方，我们在普通推理演算中将会有¬（p○p）或者p⇒¬ p。类似地，¬◇¬ p 将被¬（¬ p○¬ p）或者¬ p⇒p 代替，并且¬ ¬◇p 被p○p 或者¬（p⇒¬ p）代替。^[25]

这段描述正是我们在给出LCCS 的时候，所刻画过的东西。因此，在《符号逻辑》一书中，他认为S1 在公设上是更为经济的系统，但并不把这个S1 作为典型的严格蕴涵系统。因为这个系统的出发点乃在于：构建一个和蕴涵的通常意义一致，并且包含蕴涵普通性质的演算，由此我们才有这个S1（即系统1）。但C.I.刘易斯似乎不大喜欢这个作为普通演算系统的S1，因此在《符号逻辑》第六章的第五节，他专门讨论一致性公设，由此而构成在S1 基础上生成的S2（即系统2），这个系统也称之为“一致性演算”。

至此，我们在时间顺序上可以看到，1918年先有S3，1932年再有S1 和S2。其间的1930年，贝克（Oskar.Becker）教授发表了一篇论文，他意图找到一些公理，那些逻辑上非等价的组合公式数目可以归约为这些公理，而那些组合公式都是依据逻辑联结词“并非”和“不可能”组合起来的。贝克的这个设想，被看作是构造S4 和S5 的最初设想^[26]，这就是C.I.刘易斯《符号逻辑》附录中的第三组公设集合，C.I.刘易斯称之为C 公设集合。最早的模态系统S3 公设集合体现在1918年的《符号逻辑概论》一书中，C.I.刘易斯称之为A 公设集合。模态系统S2 公设集合，C.I.刘易斯称之为B 公设集合。由于A、B、C 这三组公设集合，我们就有了模态逻辑的S1、S2、S3、S4 和S5。

从集合A 和集合B 推演出来的每一个系统，留下了一些有关模态函项未判定的性质，这些模态函项包括◇p，¬◇p，◇¬ p，¬◇¬ p。依据这个事实，奥斯卡·贝克教授建议把以下公式考虑为进一步的公设，这些新增公设当中的任意一个或者多个可以加进每一组公设。

C10 ¬◇¬ p,¬◇¬ ¬◇¬ p ¬◇¬ ¬◇¬ p=¬◇¬ p

C11 ◇p⇒¬◇¬◇p ◇p=¬◇¬◇p

C12 p⇒¬◇¬◇p

（贝克称C12 为“布劳维尔公理”）^[27]

C.I.刘易斯5 个模态系统构建的这个时间顺序颇耐人寻味，先有S3，然后有S1 和S2，再然后有S4 和S5。观念的进化并不以时间为标准，但对系统的理解水准却是以时间为标准的。因为有了贝克的猜想之后，把贝克设想的几个公理植入到已有的C.I.刘易斯的系统之中，我们就有了S4 和S5。

2.4.3　C.I.刘易斯模态逻辑S1-S5 的生成

严格蕴涵系统S1-S5 的诞生，被称作现代逻辑历史上模态系统研究的开端。C.I.刘易斯和他的S1-S5，几乎毫无例外地放在模态逻辑这门现代逻辑学科的起点位置。模态逻辑形成早期的所谓语形传统，^[28]S1-S5 的构建过程体现的就是这种传统。我们在对S1-S5 产生的时间顺序作了以上简略描述之后，以下，我们将简要地呈现S1-S5 的生成脉络，并对这5 个模态系统特征予以简单地描述。

S1.

我们已经提及到，《符号逻辑》一书构建了严格蕴涵系统LSIS 和其等价系统LCCS。它给出了模态系统早期的初始符号、缩写定义、公理以及推理规则这些基本构成部件。但这还不是纯粹的S1。C.I.刘易斯构建的S1，称作普通推理演算，这个普通推理演算包含在1918年的严格蕴涵系统之中。产生这个普通推理演算的原因，是由于我们系统建构目标的变化。如果我们的系统建构目标旨在创建一个演绎的接近常规推理的演算，我们需要的是保留逻辑合取，即PC 的p∧q，但是，其他的一些逻辑符号，例如实质蕴涵p→q，也许还有实质析取，即所谓实质析取p∨q 都应该拒绝，因为这些符号会使得系统不必要的复杂。

这种复杂性还表现在“可能性”和“不可能性”观念上，它们在系统中也是不必要的复杂，因此也是可以去掉的。去掉这些造成系统复杂性的初始符号和基本定义的结果，就构成了S1 这种普通推理演算。以下，我们列出这个普通推理演算的基本构件。

（1）初始符号

①命题变元p、q、r 等等；

②“并非p”（¬ p）；

③“严格蕴涵”（p⇒q）；

④“严格合取”（p∧q）；

⑤“严格等值”（p≡q）。

（2）定义

①“严格析取”Def（p∨q）=¬ p⇒q；

②“一致性”Def（p○q）=¬（p⇒¬ q）；

③“严格等值”Def（p⇔q）=（p⇒q）∧（q⇒p）。

（3）公设

①（¬ p⇒q）⇒（¬ q⇒p）。（p∧q）⇒（q∧p）的等价公设。

②（p∧q）⇒p。同LSIS。

③p⇒（p∧p）。同LSIS。

④（p∧q）∧r）⇒p∧（q∧r）。同LSIS。

⑤p⇒¬（¬ p）。同LSIS。

⑥（（p⇒q）∧（q ⇒r））⇒（p⇒r）。同LSIS。

⑦（p∧（p⇒q））⇒q。同LSIS。

上述公设全部是严格蕴涵系统LSIS 中的公设，这个系统的推理规则也完全沿用LSIS 中的推理规则。

这个普通推理演算含有所有那些应用于演绎推理的实质蕴涵定理，但一定不含有无用的和可质疑的那些实质蕴涵定理，所以，C.I.刘易斯认为：

这个演算优越于实质蕴涵演算，并且，它还含有p○q这种有用的一致性关系。另一方面，它又避免了系统的复杂性，这种复杂性常被人们看作是严格蕴涵当中一个常引起异议的特性。^[29]

这样构造的S1，有一个鲜明的特点，它不能看作是PC 的扩张。因为，S1 的公理没有一个属于PC 的合式公式。并且，那些用来进行推理的规则不是PC 的推理规则，而是S1 本身的严格推理规则。^[30]

所以，尽管在1918年的《符号逻辑概论》中，C.I.刘易斯认为这个普通推理演算可行，但长期思考严格蕴涵系统的过程，改变了他对普通推理演算系统的早期看法，由此而有1932年的S2。

S2.

以上讨论的普通推理演算S1，在1932年的《符号逻辑》中稍有改变，但可以看作是和LSIS 等价。当C.I.刘易斯和朗福德在1932年用更庞大的篇幅讨论符号逻辑时，作为比PC 优越的S1，和重新建构的S2 相比，S2 更符合C.I.刘易斯对严格蕴涵系统的心仪。于是，S2 就成为他更为中意的严格蕴涵系统。

这样两个系统，还包括另外几个互为关联的其他系统（译者注：指S3、S4 和S5），这些系统将在附录2 中讨论。虽然系统1（S1）在假设上更为经济，并且，虽然在系统2（S2）中没有可用的推理法则，这些法则在系统1 中并不包含（也许在更为复杂的形式中包含），然而，我们把系统2看得更为优秀一些，因为它具有更大的简洁性。我们希望指定为是严格蕴涵系统的，正是这个系统2。^[31]

C.I.刘易斯所在意的S2 和S1 的唯一区别，是为S1 增加了一个有关可能合取的严格蕴涵公设：◇（p∧q）⇒◇p。为什么要增加这个公理构成S2？我们可以从这两个系统的比较中获得答案。

在S1 中，C.I.刘易斯把一致性（可能性）当作初始概念引入，他实际上在整个S1 中并没有对一致性和可能性做出任何说明。但严格蕴涵系统既然有一致性和可能性作为初始符号，就没有理由回避这对符号的讨论。因此，接下来，C.I.刘易斯专用一节的篇幅来讨论一致性和模态函项^[32]，而整个第四节关于一致性的讨论，自然地延伸到模态函项◇，由◇再延伸到另一个模态函项¬◇¬，不过，C.I.刘易斯的几个系统都未使用□符号。我们现在都知道，依据亚里士多德关于可能和必然之间的互为定义^[33]，这个¬◇¬ 表示为□。但在《符号逻辑》一书中，□符号并没有使用，C.I.刘易斯仅将其解释为“必然”。□符号直到1946年，才在巴坎当年的一篇论文中首次出现^[34]，然后逐渐取代可能符号◇，成为真势模态逻辑的初始模态词项。

C.I.刘易斯在该书有关一致性的讨论中，有一段关于定理18.61 的描述：命题p 是必然真的，并且我们又有断定的前提p∧q⇒r，则一定有q⇒r。用C.I.刘易斯对这个定理的说明，那就是说，在一个严格蕴涵的陈述中，人们不能够省掉一个仅仅为真的前提，这个前提是前提集合中的一个，而这个前提集合是整个地给出某个结论的。但是，人们可以省略掉一个必然真的前提。因为，在S1 之后，C.I.刘易斯把那些必然真的前提都用一个T 原则来表示。然而，当我们为S1 再增加一个严格蕴涵公设的时候，那个有点啰嗦的T 原则就可以略去不计了。

上述所有那些T 原则，它们都是从三个基本定理16.1、16.2 和16.5 推导出来的。在本章的第五节，我将表明，这三个定理，也包括那个一般的T 原则可以不用称作法则的T命题来获得证明。而去掉这个T 法则，一个进一步的公设就是必要的。^[35]

这个进一步的公设，就是有关可能合取的严格蕴涵公理：◇（p∧q）⇒◇p。S1 经过后来的修正有6 个公理，加上这个新增公理⑦，就构成了C.I.刘易斯的S2。C.I.刘易斯认为，这个S2 才典范地体现了他的严格蕴涵系统。

依据集合B1-8 演推出来的S2，含有在《符号逻辑》第六章第1-5 节中出现的所有定理，含有任意的T 原则，这些T 原则被没有T 而产生的相应定理所取代。^[36]

因为这个一致性演算系统S2 引入的一致性公理，表达的就是“可能”的性质，S2 自然也可以看成是关于可能性的推理系统。一致性或者可能性有些什么值得特别一提的性质呢？这里可以做一简单陈述。

可以看到，这里的一致性，它和我们直观语言中的一致性是等同的意义。一致性就是无矛盾性，借助于S2 的这个一致性公设，我们可以很清楚地得知：一个不可能的命题蕴涵着一对矛盾命题。但由此，也产生在实质蕴涵中出现的怪论：一个必然命题，即“不可能不p”的命题，它一定为一对矛盾命题所严格蕴涵，这表现为命题19.73。

19.73 ¬◇¬ p≡(q⇒p)∧(¬ q⇒p)

这似乎让C.I.刘易斯考虑实质蕴涵悖论的思路产生很大变化，从思考实质蕴涵出发而构思的严格蕴涵系统，那种所谓怪论的说法是来自于纯粹直观，而所谓纯粹直观并不比一致性更重要。在保证其一致性的要求之下，我们有更多处理逻辑系统的思路。于是，我们从S2 提升到S3，S2 和S3 的出现，以下我们将会看到，何以增加公理就能构成新的系统，就需要我们从语义学角度来加以关注了。

S3.

现在我们来看S3。《模态逻辑新引论》一书告诉我们，C.I.刘易斯1932年有S1 和S2，S3 在他1918年的《符号逻辑概论》中已经构造出来。^[37]C.I.刘易斯在其《符号逻辑》附录中，也有同样的断定。

在《符号逻辑概论》中，从公设集合A1-A8 演推出来的S3，含有所有S2 的定理，并且含有从A8 可推出的所有结果，例如这样的定理：

((p⇒q)∧(q⇒r))⇒(p⇒r)。

如果把B9 加进S3，则S3 包含所有S2 的存在定理。^[38]

我们知道，在S1 中增加一致性公设◇（p∧q）⇒◇p，这构成S2。

现在我们再为S2 增加一个公设：（p ⇒q）⇒（¬◇q ⇒¬◇p），这构成S3。

因为该公设涉及不可能，它可以称之为关于不可能性的公设。如果S2 是因为在S1 中增加关于可能性的一致性公设而构成的严格蕴涵系统，从表达方式上正好和S2 对应，S3 则是增加关于不可能性的不一致性公设而构成的严格蕴涵系统。

何以说，在C.I.刘易斯的1918年《符号逻辑概论》中就出现S3，节录该书第五章第一节的内容就清楚了。

本章企图在概貌上展示一种命题演算，这种演算基于“蕴涵”的一种完全不同的意义——一种在推理及证明中和蕴涵习惯用法更为一致的意义。我将称这种演算系统为严格蕴涵系统。……严格蕴涵既不是如同实质蕴涵和布尔-施罗德代数那样的外延演算，它也不是如同兰贝特（Lanbert）和卡斯提伦（Castillon）不成功的系统那样的内涵演算。它包括了两类关系，但是对这两类关系做了区分并且展示了这两类关系之间的联系。^[39]

在这个系统中，主要观念来自于麦考尔的《符号逻辑和其应用》一书，和前述S1 和S2 不同的是，它首先引入的不是一致性或者可能性的概念，而是不可能性概念，C.I.刘易斯用波浪形的符号来表示不可能。因为的引入，经典的二值逻辑变成了有五个值的逻辑。这个系统的基本构件我们简述如下，原文的一些符号我们部分做了更动，以便更符合今天的常规用法：

（1）初始符号

①命题变元p、q、r 等等；

②“并非p”（¬ p）；

③“不可能p”（ ～p）；

④“逻辑乘”（p∧q）；

⑤“严格等值”（p⇔q）。

（2）真值的五个级别

①p，表示“p 真”；

②¬ p，表示“p 假”；

③～p，表示“p 不可能”；

④¬ ～p，表示“p 不可能是假的”，也就是“p 是可能的”；

⑤～¬ p，表示“p 假是不可能的”，也就是“p 是必然的”。

（3）定义

①“一致性”：Def（p○q）=¬ ～（p∧q）；

②“严格蕴涵”：Def（p⇒q）= ～（p∧¬ q）；

③“实质蕴涵”：Def（p→q）=¬（p∧¬ q）；

④“严格逻辑加”：Def p∨q= ～（¬ p∧¬ q）；

⑤“实质逻辑加”：Def p⊻q=¬（¬ p∧¬ q）；

⑥“严格等值”：Def（p⇔q）=（ p⇒q）∧（q⇒p）；

⑦“实质等值”：Def（p≡q）=（ p→q）∧（q→p）。

以上7 种二元关系，加上逻辑乘⑧（p∧q），共有8 种二元关系，其中的逻辑乘是初始的二元观念。

把这8 种关系分为两类，一类属于实质关系，包括③、⑤、⑦和⑧。另一类属于严格关系，包括①、②、④和⑥。

（4）公设

①(p∧q)⇒(q∧p);

②(q∧p)⇒p;

③p⇒(p∧p);

④(p∧q)∧R)⇒q∧(p∧r);

⑤p⇒¬(¬ p);

⑥((p⇒q)∧(q ⇒r)),(p⇒r);

⑦～p⇒¬ p;

⑧(p⇒q)⇔( ～q⇒¬ p)。

（5）推理规则

①替换规则

A.一致性替换：

任何命题都可以用p、q、r 等命题形式任意替换，只要这种替换是一致的。

B.严格等值替换：

任意表达式都可以用一个与其严格等值的表达式置换。

②严格分离规则。

若p 被断定，并且p⇒q 被断定，则q 被断定。

③逻辑乘规则。

若p 被断定，q 被断定，则p∧q 被断定。

（6）合式公式形成规则

奇怪的是，C.I.刘易斯在推理规则的一致性替换中顺带给出合式公式的形成规则，但没有做更多的说明，也许那个时候的合式公式概念还没有出现。

①若p 是命题，则¬ p，～p 也是命题；

②若p 和q 是命题，则p∧q 也是命题。

可以看到，1918年版的这个严格蕴涵系统，正是C.I.刘易斯1932年版《符号逻辑》一书附录中给出的S3，该系统的8 个公设完全等同于附录中的公设A 集合①至⑧。从这个系统中我们可以通过降低其复杂性，去掉不可能～符号，仅用¬ 来取代，我们就可以获得S2 那个称之为不一致性的演算。而当我们把该系统中的实质蕴涵、实质逻辑加部分去掉，用一致性关系符号○来刻画纯粹的严格系统公式时，这个严格蕴涵系统就简化为S1，一个优越于实质蕴涵系统的普通推理演算。

从S3 这样一个严格蕴涵系统衍生出的S1 与S2，如果我们寻求这三个属于严格蕴涵系统S1、S2 和S3，它们得以产生的逻辑起点的话，这三个逻辑系统的起点都不是《数学原理》中的PC。它们都不是PC 的扩张，并且，这三个系统在推理规则上也和后面将要讨论到的S4 和S5 有一个明显的差别。

事实上，S1 的公理根本就没有一个公理属于PC 合式公式。而且，一致性替换规则属于PC，而S1 分离规则是针对严格蕴涵的严格分离规则，并非是针对实质蕴涵的规则。^[40]

我们曾经说过：S1 包含着PC，但又不能看作是PC 的扩张，这应该作何理解呢？我们对此作一点简要的解释。

说S1 包含着PC，仅仅是说，PC 的每一个定理同时也是S1的定理。但这不是建立在扩张的基础上，而是建立在某些导出的基础上。这样一种包含关系是以下三种导出关系的产物：

一是导出PC 的公理作为S1 的定理。

二是从S1 的推理规则导出PC 的转换推理规则，这些规则并非是初始的转换规则。

三是严格等价的含义也是导出的，在PC 中没有严格等价，PC 的等价定义并未出现在S1 中。

就C.I.刘易斯的本意而言，他意图建立一个更符合直观的逻辑系统，但需要把实质蕴涵怪论排除在外，仅仅只在PC 中有实质蕴涵怪论，而不允许同样的怪论形式包含在他的系统之中。由此，他自然不是以PC 为基础构建S3、S2 和S1，而是先构建一个S3。在他的1932年的《符号逻辑》中，这个秩序虽然发生了变化，但其本意仍在。

就此而言，C.I.刘易斯1918年在《符号逻辑概论》一书中构建的S3，可以看作是现代模态逻辑的一个起点。它向内导出了S2 和S1，构成了S1、S2 这两个严格蕴涵系统。而S3 向外扩张，借助其他逻辑学家对模态的进一步思考，形成了S4 和S5，这两个系统则成为现代正规模态逻辑的开端。

实用主义哲学家C.I.刘易斯，从对哲学思考转向对严格蕴涵的逻辑思考的结果，演化为那个时代许多逻辑学家对模态对象的思考，一个新的逻辑，非经典的模态逻辑群落由此迅速地成长起来。

S4.

在C.I.刘易斯构造严格蕴涵系统的时候，直觉主义的逻辑思想就已经出现。直觉主义逻辑不承认排中律，否定排中律的结果很容易和对模态函数的理解结合起来，因为模态函数不是提供二值，而是提供多值。正是基于这种直觉主义的逻辑观，在S3 的基础上产生了严格蕴涵系统的S4 和S5。最初的设想由奥斯卡·贝克教授在1930年的一篇讨论严格蕴涵系统的论文中提出，贝克教授考虑到这样一个公式：p⇒¬◇¬◇p，他称之为“布劳维尔公理”。

如果“并非”被翻译为“不可能”（¬◇），并且“蕴涵”被翻译为严格版的“蕴涵”，那么，直觉主义地可接受原则p→¬ ¬ p 就成为布劳维尔公理。^[41]

这就是《符号逻辑》附录中公理集合C 中的公理C12：p⇒¬◇¬◇p，它恰恰是贝克式符号翻译公设p→¬ ¬ p 的结果。而这种否定符号的替换，在C.I.刘易斯有关严格关系和实质关系的讨论中也曾提及过。C.I.刘易斯和贝克关于符号转换的讨论，本来旨在寻找出那些可以归约叠置模态的公理，布劳维尔公理C12 是其中的一个，贝克还给出公理C10、C11。

C10 ¬◇¬ p⇒¬◇¬ ¬◇¬ p

C11 ◇p⇒¬◇¬◇p

贝克给出的这三个公理，和S3 的结合，使得C.I.刘易斯的严格蕴涵系统S3，这原来是对严格蕴涵的关注，转向了一种新的关注——对模态本身的关注。由此先有S4，S4 是在S3 基础上增加贝克公理C10 的结果。

C.I.刘易斯的S3 系统加上贝克公理C10 构成的S4，是模态逻辑早期历史的一个转向。几乎是相同的时候，也就是1933年，哥德尔（Kurt Godel，1906—1978）从另外一个方向，对数学基础方向的关注而使用模态算子，他把“可证性”作为一个模态算子来解释。哥德尔在其名为《直觉主义命题演算的一个解释》的论文中，他创立一个命题连接词B 来和命题α 连接，构成模态命题Bα，表示命题α 是可证的。把这个可证性模态词B，加进经典命题逻辑PC 之中，给PC 增加相应的公理和推理规则，一个新的模态命题逻辑由此而产生，这被称为可证性逻辑。奇妙的是，这个可证性的逻辑，按照哥德尔的说法：当我们把Bα翻译为□α 的时候，它就等价于C.I.刘易斯的严格蕴涵系统S4。模态逻辑由此也才成为表达涉及信息片断的一个新真值模式的逻辑，C.I.刘易斯的严格蕴涵系统正因为和可证性逻辑的等价，而被公认为是现代模态逻辑的开端。

哥德尔式公理化风格的模态逻辑，开启了模态逻辑早期历史的转向，对这一逻辑的类别有了全新的划分。模态逻辑有了两类：一类是正规模态逻辑，一类是非正规模态逻辑。

一个模态逻辑称为正规的，如果该逻辑包括哥德尔为其可证性逻辑给出的第二个公理，□（p→q）→（□p→□q），这称之为分配公理，并且这个逻辑还有必然化规则，从├α 可导出├□α。S4 和以下将要讨论的S5，属于这样的正规模态逻辑。

而我们仔细考察过的S1-S3，则是另一类模态逻辑，称为非正规模态逻辑，它们恰恰不具有正规模态逻辑的两个必要条件——分配公理和必然化规则。同时，它们中的□模态，不具备可证的特性，而是具有可证之外的其他特性。

S5.

当把可证性看作是□模态，C.I.刘易斯称之为¬◇¬，在他最早的S3 中表示为～¬，这就构成了和哥德尔可证性逻辑等价的S4。我们按照C.I.刘易斯的思路，再来看C.I.刘易斯的S5是如何形成的。

S5，它是依据公设集合（B1-7 和C11）或者依据公设集合（B1-7 和C10，C12）推演而得。它含有S4 所有的定理，还加上C12 的逻辑后承。这样构成的严格蕴涵系统，就是C.I.刘易斯的S5。也就是说：在S3 基础上增加公理C10 ¬◇¬ p⇒¬◇¬¬◇¬ p，我们构成了S4。在S4 的基础上，再增加C11 ◇p ⇒¬◇¬◇p，我们就构成了S5。